- Dzisiejsze kompilatory optymalizują kod tak dobrze, że przeważnie działa on tak szybko jak ręcznie optymalizowany,
- Złożoność dzisiejszych procesorów i różnych poziomów pamięci jest tak wielka, że ręczna optymalizacja jest trudna,
- Procesory są tak szybkie, że większość czasu są bezczynne czekając na odczyt lub zapis danych do pamięci, urządzeń I/O.
- Kod asemblerowy jest trudny w utrzymaniu, nie przenośny
- Mały rozmiar kodu
- Programista panuje nad wszystkim, pozwala to wyeliminować niektóre zmienne czy instrukcje.
- Do kodu nie są dołączane zbędne biblioteki "standardowe".
- Można wybrać instrukcje, które są krótsze lub szybsze.
- Duża szybkość działania
- Wiedza o tym jak naprawdę działa program. Przydaje się także przy programowaniu w językach wysokiego poziomu (HLL).
- Wstawki asemblerowe.
- małe programy dla systemów wbudowanych: oprogramowanie dla telefonów, lodówek, samochodów itp.
- sterowniki urządzeń,
- wykonywanie poleceń procesora nie dostępnych w językach wysokiego poziomu, np. rotacja bitów dla kodowania,
- obliczenia wektorowe: MMX, SIMD,
- oprogramowanie które wymaga ekstremalnej wydajności: gry, pakiety algebry liniowej,
- oprogramowanie dla komputerów dla których nie istnieja języki wysokiego poziomu
- pisanie kompilatorów
- pisanie wirusów komputerowych i bootloaderów
- reverse-enginering, modyfikowanie plików wykonywalnych, łamanie zabezpieczeń
- kod samo modyfikujący się
Myśleć niskopoziomowo, pisać wysokopoziomowo.
- Randall Hyde, Profesjonalne programowanie. Część 1. Zrozumieć komputer,
- Randall Hyde,Profesjonalne programowanie. Część 2. Myśl niskopoziomowo, pisz wysokopoziomowo
- Randall Hyde, Asembler. Sztuka programowania. Wydanie II,
- Software optimization resources, Agner Fog
- NASM asembler
- Dokumentacja Intela
- Dokumentacja AMD
- 8088, 8086 (XT)
- 16 bitowe rejestry:
AX, BX, CX, DX, SI, DI, BP, SP,
CS, DS, SS, ES, IP, FLAGS - 16 bitowy tryb rzeczywisty
każdy program ma dostęp do każdej komórki pamięci. - Maksymalnie 1 MB pamięci
- Pamięć podzielona na segmenty 64K.
- 16 bitowe rejestry:
- 80286 (AT)
- 16 bitowy tryb chroniony
- Maksymalnie 16 MB pamięci, ale ciągle segmenty 64K.
- 80386, 80486, Pentium
- 32 bitowe rejestry
EAX, EBX, ECX, EDX, ESI, EDI, EBP, ESP, EIP - 32 bitowy tryb chroniony: do 4 GB pamięci.
- segmenty maksymalnie po 4GB
- 32 bitowe rejestry
- x86-64
- 64 bitowe rejestry
RAX, RBX, RCX, RDX, RSI, RDI, RBP, RSP, RIP
R8, R9, ..., R15 - Tryb 64 bitowy:
aplikacje 64 bitowe oraz 32 i 16 w trybie kompatybilności. - Adresy domyślnie 64 bitowe (obecne implementacje wykorzystują 40 bitów = 1 TB)
- Rozmiar danych: 32 bit(domyślny), 16 lub 64 bity.
- 64 bitowe rejestry
- Rejestry procesora to bardzo szybkie elementy elektroniczne, mogące przechowywać informacje (pamięć wewnętrzna procesora).
- Dostęp do nich i działania na nich są bardzo szybkie.
- Ich nazwy są zakodowane bezpośrednio w kodzie instrukcji maszynowej
MOV AX, 89 ; prześlij do rejestru AX liczbę 89 MOV DX, 10 ; prześlij do rejestru DX liczbę 10 ADD AX, DX ; dodaj 89 i 10, a wynik prześlij do AX
Przykładowy rejestr RAX
|--------------------------RAX------------------------------------|
| |------------EAX------------------|
| | |-------AX-------|
00000000000000000000000000000000|0000000000000000|00000000|00000000
| AH | AL |
GPR = General Purpose Registers
- RAX/EAX - akumulator
- najczęściej służy do wykonywania działań matematycznych na liczbach całkowitych,
- w wielu rozkazach jest domyślnym rejestrem np.
DIV BH - w tym rejestrze będziemy umieszczać numery funkcji systemu operacyjnego lub BIOSu wykonywanych po wykonaniu przerwania
MOV AH, 1 ; prześlij do rejestru AH liczbę 1 MOV AL,AH ; kopiuj AH do AL DEC AL ; odejmij 1 (dekrementacja) od AL ; AX ma wartość 256
- RBX/EBX rejestr bazowy
- często wykorzystywany po przechowywania adresu pamięci w adresowaniu pośrednim,
- używany przy dostępie do tablic jako indeks
MOV BX, 6 MOV AL, [BX] ; prześlij do rejestru AL ; zawartość pamięci spod adresu 6 MOV tablica[BX], 10 ; prześlij do 10 pod adres tablica+6
- RCX/ECX - licznik
- używany do określania ilości powtórzeń pętli
MOV CX, 5 MOV AX, 0 poczatek_petli: ; etykieta ADD AX, CX LOOP poczatek_petli ; zmniejsz CX o jeden ; i jeśli CX różne od 0 skocz do etykiety
- RDX/EDX rejestr danych
W tym rejestrze przechowujemy adresy różnych zmiennych, przesyłamy dane do przerwań.
Rejestry indeksowe
Rejestry indeksowe najczęściej służą do operacji na długich łańcuchach danych, w tym napisach i tablicach
RSI/ESI/SI indeks źródłowy
RDI/EDI/DI indeks docelowy
W trybie 32 bitowym te indeksy nie dzielą się już na 8 bitowe, w trybie 64 bitowym mamy dostęp do młodszych 8 bitów przez SIL i DIL.
Rejestry wskaźnikowe- RBP/EBP wskaźnik bazowy (base pointer)
w nim przechowuje się aktualny spód stosu dla funkcji. Pozwala to określić położenie zmiennych lokalnych. - RSP/ESP wskaźnik stosu (stack pointer)
przechowuje adres wierzchołka stosu. - RIP/EIP wskaźnik instrukcji (instruction pointer) Przechowuje adres następnej instrukcji do wykonania. Wywołanie funkcji to tak naprawdę zapamiętanie aktualnej wartości tego rejestru i zmiana na adres początku funkcji.
Rejestry segmentowe- segment kodu CS - mówi procesorowi, gdzie znajdują się dla niego instrukcje.
- segment danych DS - ten najczęściej pokazuje na miejsce, gdzie trzymamy nasze zmienne.
- segment stosu SS - dzięki niemu wiemy, w którym segmencie jest nasz stos.
- segmenty dodatkowe ES, FS, GS
Wszystkie rejestry segmentowe są 16-bitowe
W trybie 64 bitowym nie używane za wyjątkiem CS.
Aby zapisać wartość do rejestru segmentowego albo przenieść wartość pomiędzy rejestrami segmentowymi należy zrobić to pośrednio przez któryś z rejestrów ogólnego użytku.
Rejestry stanu procesoraFLAG (16-bitowe), EFLAG (32-bitowe), RFLAG (64-bitowe)
Służą one przede wszystkim do badania wyniku ostatniej operacji (na przykład czy nie wystąpiło przepełnienie, czy wynik jest zerem, itp.).
Najważniejsze flagi to :
- CF (carry flag - flaga przeniesienia),
- OF (overflow flag - flaga przepełnienia),
- SF (sign flag - flaga znaku),
- ZF (zero flag - flaga zera),
- IF (interrupt flag - flaga przerwań),
- PF (parity flag - flaga parzystości),
- DF (direction flag - flaga kierunku).
Wstęp do assembleraJęzyk maszynowy a assemblerJęzyk maszynowy wymaga instrukcji bezpośrednio jako liczb, które są rozkazami i danymi bezpośrednio pobieranymi przez procesor wykonujący ten program.
Każdy typ procesora ma swój własny język maszynowy
Asembler jest językiem programowania niskiego poziomu, co oznacza, że jednej komendzie asemblera odpowiada dokładnie jeden rozkaz procesora.
8b 15 92 80 04 08 mov edx, [koniec] eb 0a jmp koniec
- Etykieta koniec oznacza adres 0x08048092 (little endian)
Intrukcja asembleraInstrukcja assemblera ma postać:
etykieta: mnemonik operandy
- mnemoniki są charakterystyczne dla danego asemblera
- jeden mnemonic może kodować wiele instrukcji maszynowych w zależności od operandów
- kolejność i nazewnictwo operandów też jest specyficzne dla danego asemblera
Typy operandów- register - nazwa rejestru
- memory odnoszą się do danych w pamięci, adres może być podany bezpośrednio jako częśc instrukcji lub obliczany na postawie wartości rejestrów
- immediate stałe które są częścią instrukcji,
- implied operandy domyślne np. 1 w instrukcji zwiększania o jeden.
Tryby adresowania- bezpośredni - podajemy 32 bitową stałą, która określa przesunięcie względem początku pamięci (czyli adresu 0)
- pośredni przez rejestr - adres znajduje się w jednym z 32/64 bitowych rejestrów.
mov al, [eax] mov al, [ebx]
- indeksowany - efektywny adres wylicza się dodając adres zmiennej i wartość przechowywaną w jednym z rejestrów.
mov zmienna[ebx], 5
- skalowany (ModR/M)
adres = baza + indeks * skala + przesuniecie
gdzie- baza i indeks znajdują sie w rejestrach,
- skala=1,2,4,8,
- przesuniecie jest czescia instrukcji
mov [ebx + esi * 4 + 2]
- relatywny względem aktualnej instrukcji
adres = rip + przesuniecie
mov [rip + przesuniecie], 1
Typy danychRozmiary:
Nazwa Liczb bitów nasm byte 8 db word 16 dw double word (dword) 32 dd quadruple word (qword, long) 64 dq octuple word (oword) 128 do Interpretacja jest zależna od instrukcji:
- liczba całkowita bez znaku
- liczba całkowita ze znakiem
- adres pamięci
- liczba zmiennoprzecinkowa
Składnia Intel vs. AT&TIntel (NASM) neg cx add eax, 44 shl rsi, cl mov [rsp-12], edi mov dword [variable], 0 inc qword [ebp+4*ecx+32] jmp label jmp [location]
AT&T (GCC, GAS) negw %cx addl $44, %eax shlq %cl, %rsi movq %edi, -12(%rsp) movl $0, variable incq 32(%ebp,%ecx,4) jmp label jmp *location
Składnia assemblera NASMPierwsze programySekcje w linuxieWybrane sekcje zdefiniowane dla formatu elf
section .text progbits alloc exec nowrite align=16 section .data progbits alloc noexec write align=4 section .bss nobits alloc noexec write align=4 section .comment progbits noalloc noexec nowrite align=1 section other progbits alloc noexec nowrite align=1
Deklarowanie danychDo definiowania zainicjowanych danych używamy pseudoinstrukcji
db, dw, dd, dq, dt, do
w zależności od wielkości danychdb 0x55 ; just the byte 0x55 db 0x55,0x56,0x57 ; three bytes in succession db 'a',0x55 ; character constants are OK db 'hello',13,10,'$' ; so are string constants dw 0x1234 ; 0x34 0x12 dw 'a' ; 0x61 0x00 (it's just a number) dw 'ab' ; 0x61 0x62 (character constant) dw 'abc' ; 0x61 0x62 0x63 0x00 (string) dd 0x12345678 ; 0x78 0x56 0x34 0x12 dd 1.234567e20 ; floating-point constant dq 0x123456789abcdef0 ; eight byte constant dq 1.234567e20 ; double-precision float dt 1.234567e20 ; extended-precision float
Deklarowanie niezainicjowanych danychDo definiowania niezainicjowanych danych używamy
resb, resw, resd, resq, rest, reso
w zależności od wielkości danych.buffer: resb 64 ; reserve 64 bytes wordvar: resw 1 ; reserve a word realarray: resq 10 ; array of ten reals ymmval: resy 1 ; one YMM register
Deklarowanie stałychDo definiowania stałych służy equ.
message db 'hello, world' msglen equ $-message
Specjalny symbol $ ewaluuje do adresu początku obecnej lini.
Powtarzanie instrukcjiDowolną instrukcję czy pseudoinstrukcje możemy wykonać wielokrotnie dzięki times.
; inicjuje 64 bajty wartościa 0 zerobuf: times 64 db 0 ; uzupełnia buffor aby zajmował dokladnie 64 bajty bufor: db 'hello, world' times 64-$+bufor db ' '
Specjalny symbol $ ewaluuje do adresu początku obecnej lini.
NASM - instrukcjePrzenoszenie danychName Comment Syntax MOV Move (copy) MOV Dest,Source XCHG Exchange XCHG Op1,Op2 Zmiany flag procesora STC Set Carry STC CLC Clear Carry CLC CMC Complement Carry CMC STD Set Direction STD CLD Clear Direction CLD STI Set Interrupt STI CLI Clear Interrupt CLI Konwersje (rozszerza bitem znaku) CBW Sign-extend AL into AX CBW CWD Sign-extend AX into DX:AX CWD CDQ Sign-extend EAX into EDX:EAX CDQ CWDE Sign-extend AX into EAX CWDE CQO Sign-extend RAX into RDX:RAX CQO (tylko 64bit) Operacje na portach IN Input IN Dest, Port OUT Output OUT Port, Source
Stos- LIFO, rośnie w dół, skwantowany i wyrównany do 32/64 bajtów.
Jeżeli odkładamy cokolwiek to zawsze w paczkach po 32/64 bity. - RBP/EBP - przechowuje adres spodu stosu
- RSP/ESP - przechowuje adres szczytu stosu
Odkładanie na stos
push eax push rdx pushf ; odkłada flagi pusha ; odkłada wszystkie ogolne rejestry (tylko 32bit)
Przykład
jest równoważnepush rdx
sub rsp, 8 mov [rsp], rdx
Zdejmowanie ze stosu
pop ebx pop rcx popf ; zdejmuje flagi popa ; zdejmuje wszystkie ogólne rejestry ; (tylko 32bit)
Przykład
jest równoważnepop rbx
Przykład operacji na stosiemov rbx, [rsp] add rsp, 8
- RBP/EBP wskaźnik bazowy (base pointer)
Name Comment Syntax ADD Add ADD Dest,Source ADC Add with Carry ADC Dest,Source SUB Subtract SUB Dest,Source SBB Subtract with borrow SBB Dest,Source DIV Divide (unsigned) DIV Op IDIV Signed Integer Divide IDIV Op MUL Multiply (unsigned) MUL Op IMUL Signed Integer Multiply IMUL Op INC Increment INC Op DEC Decrement DEC Op CMP Compare CMP Op1,Op2 SAL Shift arithmetic left SAL Op,Quantity SAR Shift arithmetic right SAR Op,Quantity RCL Rotate left through Carry RCL Op,Quantity RCR Rotate right through Carry RCR Op,Quantity ROL Rotate left ROL Op,Quantity ROR Rotate right ROR Op,Quantity
| dest | source | source1 | Akcja |
| reg/mem8 | AX = AL*source | ||
| reg/mem16 | DX:AX = AX*source | ||
| reg/mem32 | EDX:EAX = EAX*source | ||
| reg/mem64 | RDX:RAX = RAX*source | ||
| reg16 | reg/mem16 | dest *= source | |
| reg32 | reg/mem32 | dest *= source | |
| reg16 | immed8 | dest *= immed8 | |
| reg32 | immed8 | dest *= immed8 | |
| reg16 | immed16 | dest *= immed16 | |
| reg32 | immed32 | dest *= immed32 | |
| reg16 | reg/mem16 | immed8 | dest = source*source1 |
| reg32 | reg/mem32 | immed8 | dest = source*source1 |
| reg16 | reg/mem16 | immed16 | dest = source*source1 |
| reg32 | reg/mem32 | immed32 | dest = source*source1 |
mul cl ; AX = AL*CL mul bx ; DX:AX = AX*BX mul esi ; EDX:EAX = EAX*ESI mul rdi ; RDX:RAX = RAX*RDI imul eax ; EDX:EAX = EAX*EAX imul ebx,ecx,2 ; EBX = ECX*2 imul ebx,ecx ; EBX = EBX*ECX imul si,5 ; SI = SI*5
LOGIC Name Comment Syntax NEG Negate (two-complement) NEG Op NOT Invert each bit NOT Op AND Logical and AND Dest,Source OR Logical or OR Dest,Source XOR Logical exclusive or XOR Dest,Source SHL Shift logical left SHL Op,Quantity SHR Shift logical right SHR Op,Quantity MISCELLANEOUS Name Comment Syntax NOP No operation NOP LEA Load effective adress LEA Dest,Source INT Interrupt INT Nr
Instrukcja skoku bezwarunkowego
jmp etykieta ... etykieta:
Przeważnie krótsze skoki generują krótszy kod maszynowy.
| short | 1 bajt | -128 ... +128 |
| near | 2 bajty | -32 768 ... +32 768 |
| domyślny | 4 bajty | -2 147 483 648 ... +2 147 483 648 |
Aby porównać wartości całkowitoliczbowe 80x86 dostarcza funkcji
cmp x, y
x - y i ustawia odpowiednie flagi (wynik odejmowania nie jest dostępny).
x = y : ZF = 1
Dla liczb bez znaku
x < y : ZF = 0, CF = 1 ; odejmowanie z pożyczką x > y : ZF = 0, CF = 0
Dla liczb ze znakiem
x < y : ZF = 0, OF != SF x > y : ZF = 0, OF = SF
Aby sprawdzić czy dany rejestr np. EAX jest równy zero można użyć instrukcji
test eax, eax
cmp eax, 0
W ogólności
test x, y
Wykonanie skoku zależy tylko od jednej z flag procesora
;Skok jeżeli w ostatniej operacji JZ ZF = 1 ; był wynik 0 JNZ ZF = 0 JO OF = 1 ; było przepełnienie JNO OF = 0 JS SF = 1 ; wynik był ujemny JNS SF = 0 JC SF = 1 ; przepełnienie lub niedomiar JNC SF = 0 ; dla liczb bez znaku JP PF = 1 ; najmłodszy bajt ma parzystą liczbę jedynek JNP PF = 0
Bezpośrednio po wykonaniu
cmp x, y
liczby ze znakiem liczby bez znaku skok jeżeli JE, JZ JE, JZ x = y JNE, JNZ JNE, JNZ x != y JL, JNGE JB, JNAE x < y JLE, JNG JBE, JNA x <= y JG, JNLE JA, JNBE x > y JGE, JNL JAE, JNB x >= y
- Poniższe instrukcje ułatwiają tworzenie pętli podobych do pętli for.
- Przyjmują one jako jedyny argument etykietę, do której należy wykonać skok.
- Wszystkie zmiejszają zawartość rejestru ECX o jeden.
- w jaki sposób dane będą przekazywane pomiędzy nimi: stos czy rejestry, w jakiej kolejności na stosie, w których rejestrach
- które rejestry mają być zachowane a które można zmieniać,
- kto jest odpowiedzialny za sprzątanie stosu: podprogram czy wywołujący,
- Wywołujący sprząta
- cdecl (C declaration) - konwencja języka C, parametry na stosie (RLO), wynik w EAX, Rejestry EAX, ECX, EDX można zmieniać swobodnie, pozostałe po wyjściu z podprogramu powinny być niezmienione.
- Sprząta podprogram
- pascal - parametry na stosie (LRO)
- stdcall - standardowy dla Win32 API, parametry na stosie (RLO),
- fastcall - brak jednego standardu, parametry przekazywane przez rejestry,
- Podprogram wykonujemy przez int 0x80.
- Numer funkcji systemowej w EAX
- Argumenty umieszczamy kolejno w rejestrach
ebx, ecx, edx, esi, edi, ebp
- argumentami mogą być liczby całkowite lub adresy pamięci.
- wynik zwracany jest w rejestrze EAX
- Podprogram wykonujemy przez syscall.<\li>
- Numer funkcji systemowej w RAX
- Argumenty umieszczamy kolejno w rejestrach
RDI, RSI, RDX, R10, R8, R9
- Argumentami mogą być liczby całkowite lub adresy pamięci.
- Wynik zwracany jest w rejestrze RAX.
Wartości ujemne z zakresu [-4095, -1] oznaczają błąd. - Wywołanie może niszczyć zawartość rejestrów RCX, R11.
- Argumenty są przekazywane przez stos w kolejności od prawej do lewej.
- Argumenty ze stosu musi posprzątać fukcja wywołująca.
- Wartości całkowite i adresy są zwracane w rejestrze EAX lub parze EDX:EAX, wartości zmiennoprzecinkowe zwracamy w rejestrze ST0.
- Rejestry EAX, ECX i EDX mogą zostać dowolnie zmienione przez funkcję wywołującą. Pozostałe rejestry po powrocie z fukcji muszą pozostać niezmienione.
- Rejestry zmiennoprzecinkowe ST0-ST7 przed wywołaniem funkcji i po powrocie z niej powinny być puste. Wyjątkiem jest ST0 jeżeli w nim zwracana jest wartość.
- GCC wymaga aby stos był wyrównany do granicy 16-bajtowej przed wywołaniem funkcji.
- zachowuje na stosie wartości rejestrów eax, ecx, edx (np. jeżeli przechowują liczniki pętli)
- odkłada na stos argumenty aktualne dla podprogramu w kolejności od prawej do lewej (pierwszy argument jest odkładany jako ostatni)
- wykonuje instrukcję call przekazując sterowanie do podprogramu
- wynik znajduje się w al/ax/eax/edx:eax
- po odzystaniu sterownania usuwa argumenty ze stosu (zwiększając rejestr esp)
- przywraca wartości rejestrów eax, ecx, edx jeżeli były zachowywane
- Odkładamy na stosie wartość EBP, a wartość ESP zapisuje w EBP. Nie jest to konieczne jeżeli funkcja nie korzysta ze stosu.
- Do argumentów odnosimy się relatywnie do EBP. Pierwszy znajduje się pod [EBP+8].
- Zmiejszamy ESP rezerwując pamięć na stosie dla zmiennych lokalnych. Odnosimy się do nich ponownie relatywnie do EBP.
- Odkładamy na stos wartości rejestrów, które są w podprogramie modyfikowane (poza EAX, ECX, EDX).
- Wykonujemy kod podprogramu
- Jeżeli chcemy zwrócić wartość to umieszczamy ją w rejestrze EAX (wartości zmienno-przecinkowe umieszczamy w ST0).
- Odtwarzamy wartość rejestrów.
- Odtwarzamy wartość ESP z EBP i ściągamy ze stosu poprzednią wartość EBP
- Wracamy z funkcji przez instrukcję RET
- pierwsze sześć argumentów, które są liczbami całkowitymi lub wskaźnikami (w kolejności od lewej do prawej)
są umieszczane kolejno w rejestrach
RDI, RSI, RDX, RCX, R8, R9
- Agumenty zmiennoprzecinkowe (poza
long double) są umieszczane w rejestrach SSE:XMM0, XMM1, ..., XMM7
- Rejestr
RAXpowinien zawierać liczbę liczb zmiennoprzecinkowych umieszczonych w SSE - Pozostałe argumenty są umieszczane na stosie w kolejności od prawej do lewej.
- Funkcja musi zachowywać wartość rejestrów:
RBX, RBP, RSP, R12, R13, R14, R15
- Pozostałe rejestry (w tym zmiennoprzecinkowe) mogą być dowolnie modyfikowane,
- Wynik jest umieszczany w
RAX, RDX- całkowitoliczbowy, wskaźnikXMM0,XMM1- zmiennoprzecinkowyST0,ST1- long double- pamięci pod adresem wskazanym przez RDI jeżeli zwraca się typ złożony.
- Offset pola x wynosi 0, offset pola y wynosi 4,
- Wywołując niestatyczną metodę klasy jako pierwszy parametr przekazujemy adres obiektu,
- Offset pola ma wynosi 0 w obu klasach A i B,
- Offset składowej mb jest wyrównany do granicy 4
- w funkcji check adres funkcji f jest znany na etapie kompilacji (wczesne łączenie).
- Offset pola ma wynosi 8 w obu klasach A i B (w systemach 64 bitowych),
- Offset składowej mb jest wyrównany do granicy 4
- w funkcji check adres funkcji f nie jest znany na etapie kompilacji (późne łączenie).
- Sposób reprezentownia liczb zmiennoprzecinkowych i operacje na nich określa standard IEEE 754
- Wyniki nie są dokładne: błędy zaokrągleń.
- Typy: pojedyncza precyzja (float) - 4 bajty
podwójna precyzja (double) - 8 bajtów. - Dawniej obliczenia w pojedynczej precyzji były znacząco szybsze od obliczeń w podwójnej precyzji. Obecnie różnica jest nieznaczna.
- Pierwsze procesory nie miały sprzętowego wsparcia dla liczb zmiennoprecinkowych. Musiały być realizowane przez software oparty o operacje całkowitoliczbowe.
- Koprocesor matematyczny - osobny chip, wykonuje operacje zmiennoprzecinkowe ponad 10 razy szybciej,
- Wbudowany koprocesor matematyczny od 486DX i pierwszych Pentium koprocesor jest zintegrowany z procesorem,
programowany jak oddzielny układ, Streaming SIMD Extension (SSE)
- FPU posiada 80-bitowe rejestry
ST0, ST1, ST2, ..., ST7zorganizowane w stos (LIFO). ST0zawsze wskazuje na szczyt stosu. Nowe liczby są dodawane na szczyt stosu, a pozostałe przesuwane w dół.
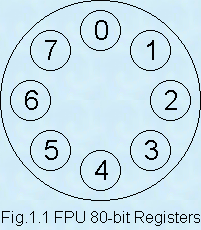
- Liczby zmiennoprzecinkowe są zawsze przechowywane jako 80-bitowe.
- Dane nie są przesuwane pomiędzy rejestrami, zmienia się tylko wskaźnik szczytu stosu.
FLD [mem32/64/80 st(n)]- umieszcza liczbę zmiennoprzecinkową pojedynczej, podwójnej lub rozszerzonej precyzji na szczycie stosu.
src może być adresem pamięci lub rejestrem koprocesora.
src nie może być rejesterem ogólnego przeznaczenia.FILD [mem16/32/64]- konwertuje liczbę całkowitą (16, 32 lub 64 bitową w pamięci) do zmiennoprzecinkowej i umieszcza na stosie.- Instrukcje ładowania stałych
FLDZ- załaduj zero. st(0) = 0.0FLD1- załaduj 1. st(0) = 1.0FLDPI- załaduj pi.FLDL2T- załaduj log2(10)FLDL2E- załaduj log2(e)FLDLG2- załaduj log(2)=log10(2)FLDLN2- załaduj ln(2)
FST [mem32/64/80 STn]- zapisz do pamięci lub rejestru STn liczbę z ST0.FSTP [mem32/64/80]- zapisz liczbę z ST0 w pamięci i zdejmij ją ze stosu. (ST1 jest przesuwany do ST0)FIST [mem16/32]- konwertuj ST0 do liczby całkowitej i zapisz do pamięci.
Sposób zaokrąglania zależy od flag koprocesora.FISTP [mem16/32/64]- jak wyżej, tylko ze zdjęciem ze stosu.FXCH STn- zamień ST0 z STn.- Dodawanie
FADD [mem32/64]ST0 += mem FADD STnST0 += STn FADD STn, ST0STn += ST0 FADDP STnFADDP STn, ST0STn += ST0. Następnie zdejmuje ST0 ze stosu. FIADD [mem32/64]ST0 += mem. Dodaje liczbę całkowitą znajdującą się w pamięci. - Odejmowanie
FSUB [mem32/64]ST0 -= mem FSUB STnST0 -= STn FSUB STn, ST0STn -= ST0 FSUBP STnFSUBP STn, ST0STn -= ST0. Następnie zdejmuje ST0 ze stosu. FISUB [mem32/64]ST0 -= mem. Odejmuje liczbę całkowitą znajdującą się w pamięci. - Odejmowanie odwrotne
FSUBR [mem32/64]ST0 = mem- ST0 FSUBR STnST0 = STn - ST0 FSUBR STn, ST0STn = ST0 - STn FSUBRP STnFSUBRP STn, ST0STn = ST0 - STn. Następnie zdejmuje ST0 ze stosu. FISUBR [mem32/64]ST0 = mem - ST0. Odejmuje od liczby całkowitej znajdującej się w pamięci wartość ST0. - mnożenie:
FMUL, składnia identyczna jak w dodawaniu. - dzielenie:
FDIV, składnia identyczna jak w odejmowaniu prostym. - dzielenie odwrotne:
FDIVR, składnia identyczna jak w odejmowaniu odwrotnym. - wartość bezwzględna:
FABS(bez argumentów) zastępuje st(0) jego wartością bezwzględną. - zmiana znaku:
FCHS: st(0) := -st(0). - pierwiastek kwadratowy:
FSQRT: st(0) := SQRT[ st(0) ] - zaokrąglanie do liczby całkowitej:
FRNDINT: st(0) := (int)st(0). - Instrukcje trygonometryczne:
FSIN- st(0) := sinus [st(0)]FCOS- st(0) := kosinus [st(0)]FSINCOS- st(0) := kosinus [st(0)], st(1) := sinus [st(0)]FPTAN- partial tangent = tangens st(0) := tg [st(0)]FPATAN- arcus tangens st(0) := arctg [st(0)]
- Logarytmiczne, wykładnicze:
FYL2Xst(1) := st(1)*log2[st(0)] i zdejmijFYL2XPIst(1) := st(1)*log2[ st(0) + 1.0 ] i zdejmijF2XM1st(0) := 2^[st(0)] - 1
- RC określa kierunek zaokrąglania wyników:
00 = Zaokrąglanie do najbliższej lub parzystej jeżeli są równo odległe (domyślny stan)
01 = Zaokrąglanie w dół (w kierunku -infinity)
10 = Zaokrąglanie w górę (w kierunku +infinity)
11 = Obcinanie (w kierunku 0) - PC określa z jaką precyzją będą przeprowadzane obliczenia
00 = 24 bits (float)
01 = nieużywany
10 = 53 bits (double)
11 = 64 bits (long double) (domyślny stan) - Exception masks określają czy ma zostać rzucony wyjątek gdy nastąpi dane zdarzenie (np. błąd przepełnienia). Domyślnie wyjątki są maskowane i oprócz ustawienia odpowiednich flag nie jest rzucany wyjątek. Przydaje się to głównie do debugowania.
- TOP określa indeks rejestru na szczycie stosu FPU
- C0,C1,C2,C3 ustawiane są przez instrukcje porównania i odpowiadają odpowiednim flagom w procesorze.
- Exception flags ustawiane są wykonane instrukcje (nie tylko ostatnią) i zawierają potencjalne błędy.
Raz ustawiona flaga musi być wyzerowana przez programistę instrukcją FCLEX WAIT/FWAIT- czekaj, aż FPU skończy pracę. Używane do synchronizacji z CPU.
Wiele z poniższych instrukcji wywołuje tą instrukcję niejawnie. Wersje z literką N nie wywołują WAITFINIT/FNINIT- inicjalizacja FPU, przywraca FPU do domyślnego stanu: ustawia flagi, czyści stos.
Dobrą praktyką jest wywoływanie go przed przystąpieniem do obliczeń (bo nie wiemy w jakim stanie inne funkcje zostawiły FPU)FLDCW,FSTCW/FNSTCW- Load/Store control word - zapisuje 16 kontrolnych bitów do pamięci, gdzie można je zmieniać na przykład aby zmienić sposób zaokrąglania liczb.FSTSW/FNSTSW- zapisz do pamięci (lub rejestru AX) słowo statusu, czyli stan FPUFCLEX/FNCLEX- wyczyść wyjątkiFLDENV,FSTENV/FNSTENV- wczytaj/zapisz środowisko (rejestry stanu, kontrolny i kilka innych, bez rejestrów danych). Wymaga 14 albo 28 bajtów pamięci, w zależności od trybu pracy procesora (rzeczywisty - DOS lub chroniony - Windows/Linux).FRSTOR,FSAVE/FNSAVE- jak wyżej, tylko że z rejestrami danych. Wymaga 94 lub 108 bajtów w pamięci, zależnie od trybu procesora.FINCSTP,FDECSTP- zwiększ/zmniejsz wskaźnik stosu - przesuń st(0) na st(7), st(1) na st(0) itd. oraz w drugą stronę, odpowiednio.FFREE- zwolnij podany rejestr danychFNOP- no operation. Nic nie robi, ale zabiera czas.FCOM st(n)/[mem]- porównaj st(0) z st(n) (lub zmienną w pamięci) bez zdejmowania st(0) ze stosu FPUFCOMP st(n)/[mem]- porównaj st(0) z st(n) (lub zmienną w pamięci) i zdejmij st(0)FCOMPP- porównaj st(0) z st(1) i zdejmij oba ze stosuFICOM [mem]- porównaj st(0) ze zmienną całkowitą 16- lub 32-bitową w pamięciFICOMP [mem]- porównaj st(0) ze zmienną całkowitą 16- lub 32-bitową w pamięci, zdejmij st(0)FCOMI st(0), st(n)- porównaj st(0) z st(n) i ustaw flagi procesora, nie tylko FPUFCOMIP st(0), st(n)- porównaj st(0) z st(n) i ustaw flagi procesora, nie tylko FPU, zdejmij st(0)- Nowe rejestry 128 bitowe XMM :
XMM0, XMM1, ..., XMM7 - 64 bitowe procesory dodają jeszcze
XMM8, ..., XMM15 - W odróżnieniu od rejestrów MMX są one zupełnie samodzielnymi rejestrami.
- SSE daje przede wszystkim możliwość wykonywania działań zmiennoprzecinkowych na 4-elementowych wektorach liczb pojedynczej precyzji (48 rozkazów).
- SSE2 – 2000 rok (wprowadzone przez firmę Intel):
- wprowadzenie działań wektorowych i skalarnych na liczbach zmiennoprzecinkowych podwójnej precyzji,
- umożliwienie wykonywania działań całkowitoliczbowych na 128-bitowych rejestrach XMM,
- większa kontrola nad pamięcią podręczną.
- SSE3 – 2004 rok (Intel):
- dodatkowe rozkazy wektorowe działające na liczbach zmiennoprzecinkowych pojedynczej i podwójnej precyzji,
- sprzętowe wspomaganie synchronizacji wątków.
- SSSE3 – 2006 rok (Intel):
- dodatkowe rozkazy wektorowe działające na liczbach całkowitych,
- rozkaz umożliwiający wyznaczenie zadanej permutacji bajtów w rejestrze XMM.
- SSE4 – 2007 rok (Intel):
- dodatkowe rozkazy wektorowe działające zarówno na liczbach całkowitych jak zmiennoprzecinkowych,
- rozkazy wektorowe wspomagające kompresję wideo,
- rozkazy wektorowe wykonujące działania na łańcuchach znaków,
- rozkazy wyznaczający sumę CRC-32.
- SSE5 – 2009 rok (AMD):
- dodatkowe rozkazy wektorowe działające zarówno na liczbach całkowitych jak zmiennoprzecinkowych,
- wprowadzenie rozkazów trój- i czteroargumentowych, w który jeden z argumentów jest docelowy (rozwiązanie z architektury RISC) – dotychczas rozkazy były 2-argumentowe, z czego jeden był równocześnie docelowy i jeśli jego wartość była potrzebna w dalszej części obliczeń, należało go zapamiętać – w rozkazach 3- i 4-arguementowych takiego problemu nie ma,
- rozkazy 4-argumentowe pozwalają akumulować wyniki mnożenia według schematu
 .
.
- Advanced Vector Extensions – 2010 rok (Intel):
- dodanie nowych, 256-bitowych rejestrów: część istniejących rozkazów SSE, SSE2, SSE3 i SSSE3, głównie zmiennoprzecinkowych może wykonywać działania na tych rejestrach,
- kilka rozkazów wektorowych działających wyłącznie na 256-bitowych rejestrach,
- część istniejących rozkazów może być wykonywana wariantach 3-argumentowych (jak w SSE5),
- rozkazy 4-argumentowe pozwalają akumulować wyniki mnożenia na liczbach zmiennoprzecinkowych według schematu
 ,
, - zwiększono z 8 do 32 liczbę relacji, które można sprawdzić rozkazami porównania (CMPPS, CMPPD),
- sprzętowe wsparcie szyfrowania AES.
- AVX2 - 2013 (Intel):
- Rozszerzenie operacji całkowitoliczbowych na rejestry YMM (256 bitowe)
- Przesunięcia bitowe
- Gather - ładowanie wektora niekoniecznie z ciągłej pamięci
- AVX-512 - 2016:
- Rozszerzenie rejestrów do 512 bitów i ich liczby do 32: ZMM0..ZMM31
- Rozszerzenie operacji aby działały dla 512 bitów
- Dodanie specjalistycznych rozszerzeń (opcjonalnych): VNNI - vector neural network instructions, GFNI - Galois field New instructions, VAES - vector AES, ...
- Typy zmiennoprzecinkowe:
- wektor 2 liczb zmiennoprzecinkowych podwójnej precyzji (2 x 64 bity)
- wektor 4 liczb zmiennoprzecinkowych pojedynczej precyzji (4 x 32 bity; wprowadzony w SSE)
- Typy całkowite (rozszerzenia typów MMX):
- wektor 16 bajtów - packed byte (16 x 8 bitów)
- wektor 8 słów - packed word (8 x 16 bitów)
- wektor 4 podwójnych słów - packed duble words (4 x 32 bity)
- wektor 2 poczwórnych słów - packed quad words (2 x 64 bity)
- liczba 128-bitowa - long quadword
- packed (równoległe) — wykonując równocześnie dwa niezależne działania zmiennoprzecinkowe na odpowiadających sobie elementach wektorów;
- scalar (skalarne) — wykonując działanie tylko na pierwszych elementach wektorów.
- MOVAPS, MOVUPS
Przesłanie 4 liczb zmiennoprzecinkowych pomiędzy rejestrem XMM, a pamięcią lub innym rejestrem XMM:
- MOVAPS — wymaga, by adres pamięci był wyrównany do granicy 16 bajtów, tj. jego 4 najmłodsze bity muszą być równe zero – w przeciwnym przypadku zgłaszany jest błąd.
- MOVUPS — nie nakłada takich ograniczeń, ale odczyt danych niewyrównanych jest zwykle wolniejszy.
- MOVSS Przesłanie jednej liczby zmiennoprzecinkowej pomiędzy rejestrem XMM, a pamięcią lub innym rejestrem XMM. Rozkaz działa na elemencie 0 rejestrów XMM: przy przesłaniach z rejestru do rejestru tylko on jest zmieniany, przy przesłaniu z pamięci do rejestru zerowane są pozostałe elementy.
- MOVLPS, MOVHPS Przesłanie 2 liczb zmiennoprzecinkowych pomiędzy rejestrem XMM i pamięcią. Rozkaz MOVLPS działa na elementach 0 i 1 rejestru XMM, natomiast MOVHPS na elementach 2 i 3.
- PD (packed double) – działanie na wektorach podwójnej precyzji,
- PS (packed single) – działanie na wektorach pojedynczej precyzji,
- SD (scalar double) – działanie na skalarach podwójnej precyzji.
- SS (scalar single) – działanie na skalarach pojedynczej precyzji.
- dodawanie (ADDPD, ADDPS, ADDSD, ADDSS)
- odejmowanie (SUBPS, SUBSS)
- mnożenie (MULPS, MULSS)
- dzielenie (DIVPS, DIVSS)
- przybliżenie odwrotności (1/x) (RCPPS, RCPSS)
- pierwiastek kwadratowy (SQRTPS, SQRTSS)
- przybliżenie odwrotności pierwiastka kwadratowego (RSQRTPS, RSQRTSS)
- wyznaczenie minimalnej wartości (MINPS, MINSS)
- wyznaczenie maksymalnej wartości (MAXPS, MAXSS)
- Może być stosowany tylko do skalarów!
- Porównują dwie liczby zmiennoprzecinkowe i ustawiają flagi procesora: rowny, mniejszy, wiekszy, nieokreslony(gdy jedna z liczb jest NaN),
COMISS, COMISD– sygnalizuje błąd gdy wystąpi nieprawidłowa liczba zmiennoprzecinkowa QNaN lub SNaNUCOMISS, UCOMISD– sygnalizuje błąd tylko w przypadku SNaN
LOOP etykieta ; wykonuje skok jeżeli ecx!=0 LOOPZ etykieta ; wykonuje skok jeżeli ecx!=0 oraz ZF=1 LOOPNZ etykieta ; wykonuje skok jeżeli ecx!=0 oraz ZF=0
mov eax, 0 mov ecx, 10 poczatek_petli: add eax, ecx loop poczatek_petli | int suma=0; for(int i=10; i!=0; --i) suma += i; |
cmp eax, ebx jle else_ mov ecx, ebx jmp koniec else_: mov ecx, eax sub ecx, ebx koniec: | if( eax>ebx ) ecx = ebx; else ecx = eax - ebx; |
mov ebx, 0 mov eax, 0 petla_start: add ebx inc ebx cmp eax, 100 jb petla_start | unsigned int b=0, suma=0; do{ suma += b; ++b; }while(suma < 100); |
mov ecx, 0 poczatek: cmp dword [tab + 4*ecx], 0 jz koniec cmp ecx, 100 jge koniec inc ecx jmp poczatek koniec: | int i=0; while(tab[i]!=0 && i<10){ i++; } |
JUMPS (general) Name Comment Syntax CALL Call subroutine CALL Proc JMP Jump JMP Dest RET Return from subroutine RET JE Jump if Equal JE Dest JZ Jump if Zero JZ Dest JCXZ Jump if CX Zero JCXZ Dest JP Jump if Parity (Parity Even) JP Dest JPE Jump if Parity Even JPE Dest JNE Jump if not Equal JNE Dest JNZ Jump if not Zero JNZ Dest JECXZ Jump if ECX Zero JECXZ Dest JNP Jump if no Parity (Parity Odd) JNP Dest JPO Jump if Parity Odd JPO Dest JUMPS unsigned (Cardinal) JA Jump if Above JA Dest JAE Jump if Above or Equal JAE Dest JB Jump if Below JB Dest JBE Jump if Below or Equal JBE Dest JNA Jump if not Above JNA Dest JNAE Jump if not Above or Equal JNAE Dest JNB Jump if not Below JNB Dest JNBE Jump if not Below or Equal JNBE Dest JC Jump if Carry JC Dest JNC Jump if no Carry JNC Dest JUMPS signed (Integer) JG Jump if Greater JG Dest JGE Jump if Greater or Equal JGE Dest JL Jump if Less JL Dest JLE Jump if Less or Equal JLE Dest JNG Jump if not Greater JNG Dest JNGE Jump if not Greater or Equal JNGE Dest JNL Jump if not Less JNL Dest JNLE Jump if not Less or Equal JNLE Dest JO Jump if Overflow JO Dest JNO Jump if no Overflow JNO Dest JS Jump if Sign (= negative) JS Dest JNS Jump if no Sign (= positive) JNS Dest
Pełne zestawy instrukcji można znaleźć na stronach INTELa i AMD.
Podstawowy zestaw instrukcji jest wspólny dla wszystkich współczesnych procesorów.
Jednakże im nowszy procesor tym ma więcej rozszerzeń.
Kod który wywołuje podprogram i podprogram muszą uzgodnić
Często takie umowy standaryzuje się jako tzw. konwencje wywołania (calling conventions)
Najczęściej spotykane konwencje 32-bitowe dla x86
Kolejność RLO (right to left order) parametrów na stosie pozwala na definiowanie funkcji o zmiennej liczbie parametrów np. printf. W tym wypadku funkcja nie może sprzątać!
Funkcja wywołująca:
; b = f(a, 5) push ecx ; zachowujemy licznik pętli mov eax, 5 ; odkładamy argumenty na stos push eax ; w odwrotnej kolejności mov eax, [a] push eax call f ; wywołujemy funkcję add esp, 8 ; czyścimy stos mov [b], eax ; zapisujemy wynik pop ecx ; przywracamy licznik pętli
Podprogram może swobodnie modyfikować rejestry EAX, ECX, EDX pozostałe po wyjściu z podprogramu powinny być niezmienione.
int f(int a, int b){ int c = a+b; return c; }
; zwraca sumę a+b f: push ebp ; zachowujemy starą wartość ebp mov ebp, esp sub esp, 4 ; przydzielamy pamięć na zmienna lokalna c mov eax, [ebp+8] ; mov eax, [a] add eax, [ebp+12] ; add eax, [b] mov [ebp-4], eax ; mov [c], eax ; wynik jest juz w eax mov esp, ebp ; zwolnienie pamięci na stosie pop ebp ; przywrócenie poprzedniej wartości ebp ret ; powrót
Zawartość stosu
[ebp+12] b [ebp+8] a [ebp+4] adres powrotu z funkcji [ebp] poprzednia wartość ebp [ebp-4] zmienna lokalna c
Przyklad cdecl ze stosem 64 bitowym
Instrukcje ENTER i LEAVE tworzą i usuwają ramkę stosu.
Instrukcja
enter rozmiar, 0
push ebp mov ebp, esp sub esp, rozmiar
Instrukcja
leave
mov esp, ebp pop ebp
Przy ich użyciu funkcja f ma postać
; zwraca sumę a+b f: enter 4,0 ; utworzenie ramki stosu mov eax, [ebp+8] ; mov eax, [a] add eax, [ebp+12] ; add eax, [b] mov [ebp-4], eax ; mov [c], eax ; wynik jest juz w eax leave ; usunięcie ramki stosu ret ; powrót
Większość kompilatorów C poprzedza nazwy funkcji znakiem podkreślenia np. funkcja suma będzie
w assemblerze miała nazwę _suma. Kompilator GCC jest tu wyjątkiem: nazwy są dokładnie takie same.
W pliku C deklarujemy funkcję jako zewnętrzną
extern int suma(int, int);
W pliku assemblerowym musimy odpowiedni symbol zdefiniowac jako globalny, aby był widoczny w innych jednostach kompilacji
global suma suma: ; tutaj cialo funkcji ret
Następnie kompilujemy każdy plik osobno i linkujemy razem.
Program w C
Moduł w assemblerze
Jeżeli w naszej funkcji asemblerowej nie bedziemy przestrzegać przyjętej konwencji, to może to doprowadzić do trudnego do zrozumienia dziwnego zachowania programu.
Jeżeli zmienimy wartość jednego z rejestrów, które nie powinny być modyfikowane przez funkcje wywołaną to tak jak gdybyśmy zmieniali zmienne lokalne funkcji wywołującej.
Przykład
Program w C
Moduł w assemblerze
W trybie 64 bitowym parametry są przekazywane w pierwszej kolejności nie przez stos ale przez rejestry. Znacznie przyspiesza to wywołanie funkcji.
Przykładowo dla funkcji
int suma(int a, int b);
RDI, b natomiast w RSI wynik zwrócony zostanie w RAX.
Program w C
Moduł w assemblerze
| Funkcja | Parametry |
|---|---|
int f(int a,
double b,
double c,
int d,
float e,
long double f,
char g,
long h,
int * i,
double * j,
int k,
char l); |
RDI XMM0 XMM1 RSI XMM2 stos RDX RCX R8 R9 stos stos |
Uwaga: Jeżeli przesyłamy przez wartość prostą strukturę to jest ona też umieszczana w rejestrach.
typedef struct { int a; int b; } Dane; extern int suma(Dane); ... Dane dane; int c = suma(dane);
W rejestrze RDI zostanie przesłana cała struktura dane.
W starszych 4 bajtach bedzie dane.a, a w młodszych dane.b.
Wynik zwracamy w RAX
Program w C
Moduł w assemblerze
Jeżeli zwracamy przez wartość prostą strukturę to jeżeli zmieści się ona w rejestrach
RAX,RDX,XMM0,XMM1 to tam należy ją umieścić.
Uwaga: musi to już być program C++ bo czyste C nie pozwala zwracać struktur z funkcji.
typedef struct { int a; int b; } Dane; extern "C" Dane suma(Dane); ... Dane dane; Dane c = suma(dane);
W rejestrze RDI zostanie przesłana cała struktura dane.
W starszych 4 bajtach bedzie dane.a, a w młodszych dane.b.
Wynik zwracamy w RAX
Program w C
Moduł w assemblerze
Jeżeli zwracamy przez wartość dużą strukturę i nie zmieści się ona w rejestrach
RAX,RDX,XMM0,XMM1 to do funkcji w RDI zostanie przesłany adres gdzie należy umieścić wynik.
typedef struct { int a, b, c, d, e; } Dane; extern "C" Dane suma(int, int); ... Dane c = suma(4, 5);
W rejestrze RDI zostanie przesłany adres zmiennej c.
W RSI będzie wartość 4, a w RDX wartość 5.
Wynik wpisujemy bezpośrednio do zmiennej c, a w RAX zwracamy adres zmiennej c
Program w C
Moduł w assemblerze
W C++ można zdefiniować kilka funkcji o tej samej nazwie
void f(); int f(int n); double f(double x, double y);
Co więc oznaczałoby:
call f
// Funkcja void f(); void f(int x); void f(double x); void f(int * x); double f(int x, double y); double f(int (*fun)(int), int); void Klasa::f(int i, double t); static void Klasa::f(int i); | ; Nazwa
_Z1fv
_Z1fi
_Z1fd
_Z1fPi
_Z1fid
_Z1fPFiiEi
_ZN5Klasa1fEid
_ZN5Klasa1fEi |
Nazwa jest zależna od systemu, kompilatora. Reguły są dość skomplikowane.
Zamiast zgadywać nazwę można zobaczyć jaką nazwę używa kompilator.
g++ -S plik.cpp -o plik.asm
Jeżeli chcemy format bardziej podobny do NASMa to należy dodać opcję -masm=intel.
g++ -masm=intel -S plik.cpp -o plik.asm
void f(); // 1 void f(int x); // 2 void f(double x); // 3 void f(int * x); // 4 double f(int x, double y); // 5 class Klasa { public: void f(int i, double t); // 6 static void f(int i); // 7 }; int main(){ int x=1; double y=1.1; f(); f(x); f(y); f(&x); f(x,y); Klasa k; k.f(x,y); Klasa::f(x); } | main: push ebp mov ebp, esp and esp, -16 sub esp, 32 mov DWORD PTR [esp+24], 1 fld QWORD PTR .LC0 fstp QWORD PTR [esp+16] call _Z1fv ; (1) mov eax, DWORD PTR [esp+24] mov DWORD PTR [esp], eax call _Z1fi ; (2) fld QWORD PTR [esp+16] fstp QWORD PTR [esp] call _Z1fd ; (3) lea eax, [esp+24] mov DWORD PTR [esp], eax call _Z1fPi ; (4) mov eax, DWORD PTR [esp+24] fld QWORD PTR [esp+16] fstp QWORD PTR [esp+4] mov DWORD PTR [esp], eax call _Z1fid ; (5) fstp st(0) mov eax, DWORD PTR [esp+24] fld QWORD PTR [esp+16] fstp QWORD PTR [esp+8] mov DWORD PTR [esp+4], eax lea eax, [esp+31] mov DWORD PTR [esp], eax call _ZN5Klasa1fEid ; (6) mov eax, DWORD PTR [esp+24] mov DWORD PTR [esp], eax call _ZN5Klasa1fEi ; (7) mov eax, 0 leave ret .LC0: .long 2576980378 .long 1072798105 |
Przykładowy plik C++
Odpowiadający mu plik asemblerowy (GAS)
Porównajmy dwa sposoby inicjowania struktury
typedef struct { int a; int b; char c; double d; double e; } Dane;
Dane init(){ Dane d; d.a = 1; d.b = 2; d.c = A; d.d = 1.244; d.e = 2.345; return d; } int main(){ Dane d = init(); return 0; } | void init(Dane * d){ d->a = 1; d->b = 2; d->c = 'A'; d->d = 1.244; d->e = 2.345; } int main(){ Dane d; init(&d); return 0; } |
Niebezpieczeństwo w pierwszym kodzie polega na tym, że pomimo iż do funkcji jest przekazywany adres struktury d,
to w funkcji zostanie utworzony lokalny obiekt i na końcu funkcji będzie potrzebne skopiowanie go.
W C++ nie mamy w funkcji init jawnego dostępu do obiektu w którym zwracamy wartość.
Obecne kompilatory potrafią wygenerować wydajny kod nawet bez optymalizacji.
Pierwszy program (Pokaż/ukryj kod)
#include <stdio.h> typedef struct { int a; int b; char c; double d; double e; } Dane; Dane init(){ Dane d; d.a = 1; d.b = 2; d.c = 'A'; d.d = 1.244; d.e = 2.345; return d; } int main(){ Dane d = init(); return 0; }
Kod asemblerowy wygenerowany przez gcc
Drugi program (Pokaż/ukryj kod)
#include <stdio.h> typedef struct { int a; int b; char c; double d; double e; } Dane; void init(Dane * d){ d->a = 1; d->b = 2; d->c = 'A'; d->d = 1.244; d->e = 2.345; } int main(){ Dane d; init(&d); return 0; }
Kod asemblerowy wygenerowany przez gcc
Przekazywanie argumentów przez referencje w C++ jest równoważne w assemblerze przekazywaniu wskaźnika zmiennej.
void fun(int * x) { *x = 1; } void fun(int & x) { x = 1; } int main() { int x = 0; fun(&x); fun(x); } | _Z3funPi: push ebp mov ebp, esp mov eax,[ebp+8] mov [eax], 1 pop ebp ret _Z3funRi: push ebp mov ebp, esp mov eax, [ebp+8] mov [eax], 1 pop ebp ret global main main: push ebp mov ebp, esp sub esp, 20 mov [ebp-4], 0 lea eax, [ebp-4] mov [esp], eax call _Z3funPi lea eax, [ebp-4] mov [esp], eax call _Z3funRi mov eax, 0 leave ret |
Referencje są tylko udogodnieniem w sposobie zapisu, zwłaszcza przy przeciążaniu operatorów np. a + b zamiast &a + &b .
Funkcje inline są z założenia krótkimi funkcjami, dla których w miejscu wywołania wkleja się ich ciało zamiast robić skok do podprogramu.
Funkcje te miały zastąpić makra preprocesora.
Funkcje inline poprzedzamy w C++ słowem kluczowym inline. Jest to jednak tylko sugestia dla kompilatora.
Ciało takiej funkcji kompilator musi znać w momencie kompilacji dlatego najczęściej umieszcza się je w plikach nagłówkowych.
int kwadrat(int x){ return x*x; } inline int kwadrat_inline(int x){ return x*x; } int main(){ int x = 5, y ; y = kwadrat(x); y = kwadrat_inline(x2); } | _Z7kwadrati: push ebp mov ebp, esp mov eax, [ebp+8] imul eax, [ebp+8] pop ebp ret main: push ebp mov ebp, esp and esp, -16 sub esp, 32 mov [esp+28], 5 mov eax, [esp+28] push eax call _Z7kwadrati mov [esp+24], eax mov eax, [esp+28] imul eax, [esp+28] mov [esp+24], eax mov eax, 0 leave ret |
W praktyce kompilator GCC w tym przypadku nie inline'ował funkcji, a przy włączonej optymalizacji po prostu obliczał jej wartość
class A{ public: int x; int y; void f(){ x=1; } }; int main(){ A a a.y = 3; a.f(); } | main: push rbp ; ramka stosu mov rbp, rsp sub rsp, 16 mov DWORD [rbp-12], 3 ; a.y = 3 lea rax, [rbp-16] ; przesylamy adres a mov rdi, rax ; jako pierwszy parametr call _ZN1A1fEv ; metody f mov eax, 0 leave ret |
class A{ public: char ma; void f(){ cout << "\n f w A \n" ; } }; class B : public A { public: int mb; void f(){ cout << "\n f w B \n" ; } }; void check( A * p){ p->ma = 3; p->f(); } | _Z5checkP1A: push rbp mov rbp, rsp mov rax, rdi mov byte [rax], 3 call _ZN1A1fEv leave ret |
class A{ public: char ma; virtual void f(){ cout << "\n f w A \n" ; } }; class B : public A { public: int mb; void f(){ cout << "\n f w B \n" ; } }; void check( A * p){ p->ma = 3; p->f(); } | _Z5checkP1A: push rbp mov rbp, rsp sub rsp, 16 mov rax, rdi mov BYTE [rax+8], 3 mov rax, [rax] mov rdx, [rax] call rdx leave ret |
Jeżeli klasa bazowa i potomna nie mają funkcji wirtualnych to obiekty nie posiadają wskaźników do tablicy funkcji wirtualnych.
class A { public: int a; }; class B : public A { public: int b; }; | A --> +---------+
| a |
+---------+
B --> +---------+
| a |
+---------+
| b |
+---------+ |
Jeżeli w klasie są obecne funkcje wirtualne to obiekt posiada wskaźnik do tablicy funkcji wirtualnych.
class A { public: int a; virtual void v(); }; class B : public A { public: int b; virtual void w(); void f(); };
+-----------------+
| 0 (top_offset) |
B ------------------+ typeinfo
>+--------+ | wsk do typeinfo |----> dla B
| vtable |---> +-----------------+
+--------+ | * A::v() |----> A::v(){}
| a | +-----------------+
+--------+ | * B::w() |----> B::w(){}
| b | +-----------------+
+--------+
Jeżeli w klasie B nadpiszemy funkcję v to w vtable zmieni się wskaźnik.
class A { public: int a; virtual void v(); }; class B : public A { public: int b; void v(); virtual void w(); void f(); };
+-----------------+
| 0 (top_offset) |
B ------------------+ typeinfo
>+--------+ | wsk do typeinfo |----> dla B
| vtable |---> +-----------------+
+--------+ | * A::v() |--+ A::v(){}
| a | +-----------------+ +-> B::v(){}
+--------+ | * B::w() |----> B::w(){}
| b | +-----------------+
+--------+
class A { public: int a; virtual void v(); }; class B { public: int b; virtual void w(); }; class C : public A, public B { public: int c; };
+-----------------------+
| 0 (top_offset) |
+-----------------------+
c --> +----------+ | ptr to typeinfo for C |
| vtable |-------> +-----------------------+
+----------+ | A::v() |
| a | +-----------------------+
+----------+ | -8 (top_offset) |
| vtable |---+ +-----------------------+
+----------+ | | ptr to typeinfo for C |
| b | +---> +-----------------------+
+----------+ | B::w() |
| c | +-----------------------+
+----------+
class A { public: int a; virtual void v(); }; class B : public A { public: int b; virtual void w(); }; class C : public A { public: int c; virtual void x(); }; class D : public B, public C { public: int d; virtual void y(); };
+-----------------------+
| 0 (top_offset) |
+-----------------------+
d --> +----------+ | ptr to typeinfo for D |
| vtable |-------> +-----------------------+
+----------+ | A::v() |
| a | +-----------------------+
+----------+ | B::w() |
| b | +-----------------------+
+----------+ | D::y() |
| vtable |---+ +-----------------------+
+----------+ | | -12 (top_offset) |
| a | | +-----------------------+
+----------+ | | ptr to typeinfo for D |
| c | +---> +-----------------------+
+----------+ | A::v() |
| d | +-----------------------+
+----------+ | C::x() |
+-----------------------+
class A { public: int a; virtual void v(); }; class B : public virtual A { public: int b; virtual void w(); }; class C : public virtual A { public: int c; virtual void x(); }; class D : public B, public C { public: int d; virtual void y(); };
+-----------------------+
| 20 (vbase_offset) |
+-----------------------+
| 0 (top_offset) |
+-----------------------+
| ptr to typeinfo for D |
+----------> +-----------------------+
d --> +----------+ | | B::w() |
| vtable |----+ +-----------------------+
+----------+ | D::y() |
| b | +-----------------------+
+----------+ | 12 (vbase_offset) |
| vtable |---------+ +-----------------------+
+----------+ | | -8 (top_offset) |
| c | | +-----------------------+
+----------+ | | ptr to typeinfo for D |
| d | +-----> +-----------------------+
+----------+ | C::x() |
| vtable |----+ +-----------------------+
+----------+ | | 0 (vbase_offset) |
| a | | +-----------------------+
+----------+ | | -20 (top_offset) |
| +-----------------------+
| | ptr to typeinfo for D |
+----------> +-----------------------+
| A::v() |
+-----------------------+
Realizacja tablic funkcji wirtualnych zależy od tego jakie są klasy bazowe danej klasy. Jest to też często specyficzne dla danego kompilatora
Dobrą prezentację można znaleźć pod adresem
http://tinydrblog.appspot.com/?p=89001
Lokalna kopia strony
Itanium C++ ABI - można tam znaleźć wiele szczegółów implementacyjnych różnych konstrukcji C++.
Wszystkie instrukcje FPU poprzedzone są przedrostkiem F.
Instrukcje które zdejmują wartość ze stosu mają przyrostek P, jeżeli zdejmują dwie wartości to PP
Wynik działań jest zawsze umieszczany w jednym z rejestrów.
Przykład
Plik asemblerowy
Plik C
FPU control word pozwala na zmianę ustawień FPU
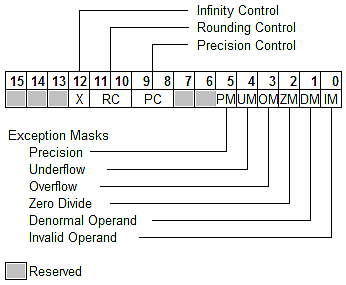
FPU status word zawiera aktualny stan FPU:
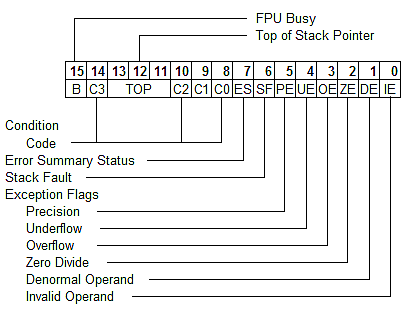
FPU oprócz rejestrów danych zawiera także rejestr
kontrolny (16 bitów) i rejestr stanu (16 bitów).
W rejestrze stanu są 4 bity nazwane
C0, C1, C2 i C3. To one wskazują wynik ostatniego porównania, a układ ich jest taki sam,
jak flag procesora, co pozwala na ich szybkie przeniesienie do flag procesora.
Aby odczytać wynik porównania, należy przenieść rejestr flag z koprocesora do procesora:
fcom ; porównujemy fstsw ax ; kopiujemy rejestr flag koprocesora do ax sahf ; AH zapisane do flag
Następnie możemy używać rozkazów skoków tak jak dla liczb całkowitych bez znaku: JE, JB itp.
Komendy kończące się na I lub IP zapisują swój wynik bezpośrednio do flag procesora.
Można tych flag od razu używać (JZ, JA, ...). Te komendy są
dostępne od Pentium Pro.
FTST porównuje st(0) z zerem.
FXAM bada, co jest w st(0) - prawidłowa liczba, błąd
(NaN = Not a Number), czy 0.
| Rodzaj liczby | C3 | C2 | C0 |
|---|---|---|---|
| Błędna liczba | 0 | 0 | 0 |
| NaN | 0 | 0 | 1 |
| Zwykła liczba skończona | 0 | 1 | 0 |
| Nieskończoność | 0 | 1 | 1 |
| Zero | 1 | 0 | 0 |
| Pusty rejestr | 1 | 0 | 1 |
| Liczba zdenormalizowana | 1 | 1 | 0 |
Rejest C1 zawiera znak liczby w ST0
SSE = Streaming SIMD Extension SIMD = Single Instruction Multiple Data
SSE to dodatkowe rozkazy, które pozwalają znacznie szybciej wykonywać obliczenia matematyczne, szczególnie te wykorzystywane w dziedzinie multimediów, co przekłada się na zwiększenie efektywności działania m.in. gier komputerowych, programów graficznych, muzycznych, kodowania filmów i muzyki.
Materiały pochodzą z polskiej Wikipedii i serwisu Ważniak
Rozkazy SSE mogą wykonywać działania arytmetyczne na wektorach liczb zmiennoprzecinkowych na dwa sposoby:
Przykład – mnożenie dwóch wektorów (rozkazem MULPS xmm0, xmm1):
+-------+-------+-------+-------+ | x3 | x2 | x1 | x0 | xmm0 +-------+-------+-------+-------+ * * * * +-------+-------+-------+-------+ | y3 | y2 | y1 | y0 | xmm1 +-------+-------+-------+-------+ = = = = +-------+-------+-------+-------+ | x3*y3 | x2*y2 | x1*y1 | x0*y0 | xmm0 +-------+-------+-------+-------+
Przykład – mnożenie pierwszych elementów wektorów (rozkazem MULSS xmm0, xmm1 ):
+-------+-------+-------+-------+ | x3 | x2 | x1 | x0 | xmm0 +-------+-------+-------+-------+ * +-------+-------+-------+-------+ | y3 | y2 | y1 | y0 | xmm1 +-------+-------+-------+-------+ = = = = +-------+-------+-------+-------+ | x3 | x2 | x1 | x0*y0 | xmm0 +-------+-------+-------+-------+
Przykład – mnożenie dwóch wektorów (rozkazem MULPD xmm0, xmm1):
+-------+-------+-------+-------+ | x1 | x0 | xmm0 +-------+-------+-------+-------+ * * * * +-------+-------+-------+-------+ | y1 | y0 | xmm1 +-------+-------+-------+-------+ = = = = +-------+-------+-------+-------+ | x1*y1 | x0*y0 | xmm0 +-------+-------+-------+-------+
Dla nazw instrukcji sufiks nazwy określa typ:
Dla tych elementów, dla których wynik porównania jest prawdziwy wszystkie bity w rejestrze docelowym są ustawiane, gdy nieprawdziwy – zerowane. Ten sposób porównania może być zastosowany zarówno dla wektorów (rozkaz CMPPS) jak i skalarów (rozkaz CMPSS)
Przykład testowania, czy liczby są różne (rozkaz CMPNEQPS xmm0, xmm1[1]):
+---------+---------+---------+---------+
| 1.0 | -5.3 | 16.5 | 17.2 | xmm0
+---------+---------+---------+---------+
≠ ≠ ≠ ≠
+---------+---------+---------+---------+
| 7.0 | -5.3 | 16.5 | 17.3 | xmm1
+---------+---------+---------+---------+
= = = =
+---------+---------+---------+---------+
|111..1111|000..0000|000..0000|111..1111| xmm0
+---------+---------+---------+---------+
- Ustawienia operacji zmiennoprzecinkowych:
- sposób zaokrąglanie wyniku:
- do najbliższej liczby całkowitej
- zaokrąglanie w stronę plus nieskończoności
- zaokrąglanie w stronę minus nieskończoności
- ucinanie (zaokrąglanie w stronę zera)
- flaga flush-to-zero – jeśli ustawiona w przypadku niedomiaru zamiast zgłaszania wyjątku, zapisywana jest liczba zero; działanie nie jest zgodne ze standardem, ale powoduje przyspieszenie programów
- sposób zaokrąglanie wyniku:
- Maski włączające zgłaszanie wyjątków przy błędach; wykrywane błędy:
- niewłaściwe argumenty (np. pierwiastkowanie ujemnej liczby),
- dzielenie przez zero,
- nadmiar (wynik jest zbyt duży),
- niedomiar (wynikiem jest liczba nie znormalizowana),
- niedokładny wynik (wynik nie może być dokładnie reprezentowany).
- Flagi wskazujące rodzaj błędu – ustawiane automatycznie przez procesor, niezależnie od tego, czy dany błąd jest zgłaszany, czy nie; muszą zostać wyzerowane programowo (zwykle w procedurze obsługi wyjątków SSE).
Dane nie wyrównane
Dane wyrównane
Funkcje liczące iloczyn
SSE_u - SSE dane nie wyrównane
SSE_a - SSE dane wyrównane
FPU - kooprocesor numeryczny
C++ - implementacja w C++ używa SSE ale nie wektorowo.
C++(-O2) - implementacja w C++ z optymalizacją używa SSE wektorowo.
Test 1: duże tablice
Test 3: małe tablice
Wyniki Pentium Core 2 Duo
| SSE_u | SSE_a | FPU | C++ | C++(-O2) | |
|---|---|---|---|---|---|
| Test 1 | 28.5 | 28.0 | 29.3 | 55.3 | 27.7 |
| Test 2 | 0.63 | 0.31 | 1.03 | 5.05 | 0.31 |
Wyniki Pentium Core i7
| SSE_u | SSE_a | FPU | C++ | C++(-O2) | |
|---|---|---|---|---|---|
| Test 1 | 8.04 | 8.02 | 8.04 | 30.44 | 8.04 |
| Test 2 | 1.343 (1.557) | 1.243 | 5.221 | 29.923 | 4.790 |
- Przy operacjach wektorowych na liczbach całkowitych może dojść do przepełnienia i "zawinięcia wyniku", co powoduje dużą niedokładność.
- Operacje dodawania i odejmowania z nasyceniem w przypadku nadmiaru lub niedomiaru zwracają odpowiednio wartość maksymalna i minimalna dla danego typu.
- Istnieją odpowiednie instrukcje dla liczb ze znakiem: PADDS, PSUBS oraz bez znaku PADDUS, PSUBUS
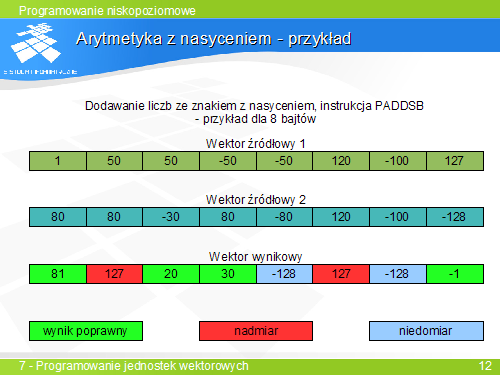
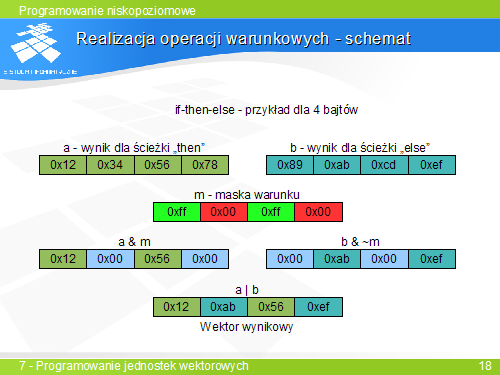
- Chcemy wykonać różne operacje dla różnych elementów wektora w zależnośći od spełnienia dla danych elementów pewnego warunku.
- Chcemy uniknąć instrukcji if która znacznie spowalnia.
Rozwiązanie:
- Wektorowe operacje logiczne zwracają maski bitowe M (dla elementów dla których warunek był spełniony na odpowiednim miejscu są same jedynki).
- obliczamy dwie możliwe wartości wyniku : Vt - dla przypadku spełnienia warunku i Vf dla niespełnienia.
- Wykonujemy iloczyn logiczny Vt z maską M i odpowiedznio Vf z ~M
- Ostateczny wyniki jest sumą logiczna tych wyników
(Vt & M) | (Vf & ~M)
section .data const40 'MMMMMMMMMMMMMMMM' star '****************' section .text ; if(x <= 'M') x = '*'; sse_if: movdqu xmm0, [rdi] ; MOVe Double Quadword [Aligned] movdqu xmm1, [const40] ; wektor stałych 40 movdqa xmm2, xmm0 ; pcmpgtb xmm2, xmm1 ; xmm2 zawiera maske movdqa xmm1, [star] pand xmm0, xmm2 ; zerujemy znaki mniejsze niż M pandn xmm2, xmm1 ; ustawiamy tam gwiazdki por xmm0, xmm2 ; sumujemy movdqu [rdi], xmm0 ret
Przykład
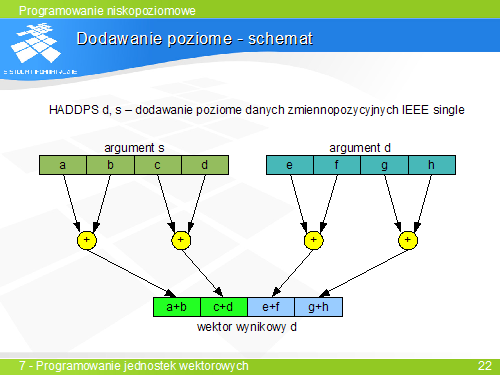

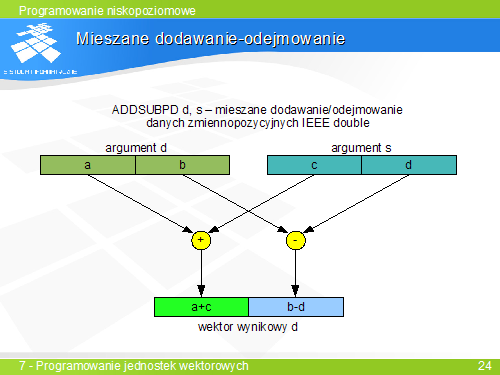
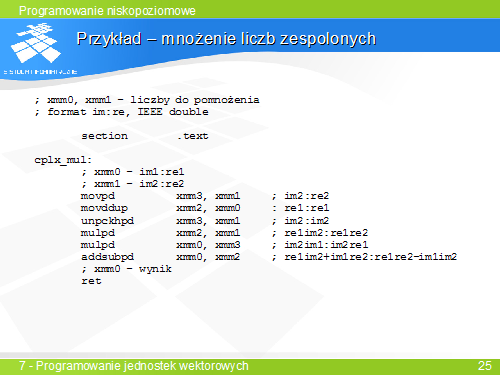
Do pracy z tablicami/łańcuchami przeznaczone są specjalne instrukcje (string instructions). W mnemoniku przeważnie pojawia się literka S.
Używają one rejestrów
- ESI do wskazania adresu źródłowego (source)
- EDI do wskazania adresu docelowego (destination).
Flagi modyfikujemy przez
- CLD zeruje flagę DF (rejestry będą zwiększane).
- STD ustawia flagę DF (rejestry będą zmiejszane).
Zakładamy że flaga DF jest wyzerowana. W przeciwnym wypadku rejestry są zmiejszane.
Instrukcja LODSB/LODSW/LODSD STOSB/STOSW/STOSD MOVSB/MOVSW/MOVSD | "Odpowiednik" mov AL/AX/EAX, [DS:ESI] add ESI, 1/2/4 mov [ES:EDI], AL/AX/EAX add EDI, 1/2/4 mov [ES:EDI], [DS:ESI] ; 1,2 lub 4 bajty add ESI, 1/2/4 add EDI, 1/2/4 |
W trybie chronionym mamy tylko jeden segment danych więc nie musimy się przejmować wartością rejestrów ES i DS.
; kopiuje tablice zrodlo o rozmiarze n do tablicy cel ; copyArray(int n, int zrodlo[], int cel[]); copyArray: enter 0,0 cld ; zerujemy flagę DF mov ecx, [ebp+8] ; rozmiar tablicy mov esi, [ebp+12] ; zrodlo mov edi, [ebp+16] ; cel petla: lodsd stosd loop petla leave ret
Główną pętlę można też uprościć
petla: movsd loop petla
Instrukcje CMPSx służą do porównywania kolejnych komórek dwóch tablic jako liczb 1, 2 lub 4 bajtowych.
Instrukcja CMPSB CMPSW CMPSD | "Odpowiednik" cmp [DS:ESI], [ES:EDI] add ESI, 1/2/4 add EDI, 1/2/4 |
Instrukcje SCASx przeszukują tablicę w poszukiwaniu konkretnej wartości umieszczonej w rejestrze EAX
Instrukcja SCASB SCASW SCASD | "Odpowiednik" cmp AL/AX/EAX, [ES:EDI] add EDI, 1/2/4 |
Przykład: szukanie elementu w tablicy liczb typu int
cld mov edi, tablica ; adres poczatku tablicy mov ecx, [rozmiar] ; rozmiar tablicy mov eax, [liczba] ; liczba ktorej szukamy petla: scasd je znaleziono loop petla ; nie znaleziono jmp koniec znaleziono: sub edi, 4 ; edi wskazuje teraz na miejsce ;gdzie znajduje się szukany element koniec: ... segment .data tablica dd 1, 2, 3, 4, 5, 6, 7 rozmiar dd 7 liczba dd 4
Przedrostki REPx informują procesor, że ma wykonywać daną instrukcję tablicową określona liczbę razy, ewentualnie sprawdzając dodatkowy warunek.
Liczbę powtórzeń umieszczamy w rejestrze ECX
REP ; powtarza instrukcje ECX razy REPE/REPZ ; powtarza instrukcję jeżeli flaga ZF jest ustawiona, ; conajwyżej ECX razy REPNE/REPNZ ; powtarza instrukcję jeżeli flaga ZF jest wyzerowana, ; conajwyżej ECX razy
Przykład: kopiowanie tablicy
cld mov esi, zrodlo mov edi, cel mov ecx, [rozmiar] rep movsd
Przykład: porównanie dwóch tablic
cld mov esi, tablica1 mov edi, tablica2 mov ecx, [rozmiar] repe cmpsb ; powtarzaj jeżeli są równe je rowne ; jeżeli ZF==0 to tablice są rowne ; blok kodu gdy tablice są różne jmp koniec rowne: ; blok kodu gdy tablice są takie same koniec:
Główne różnice pomiędzy składnią Intela a AT&T
- Zmieniona kolejność operandów : najpierw źródło potem cel
OpCode źrodlo, cel
- Nazwy rejestrów poprzedzamy % np. %eax, %ebx
- Stałe poprzedzamy znakiem $, stałe szesnastkowe przez $0x
$1, $322, $0xffff
-
Rozmiar operandów określamy dodając do OpCode przyrostek: b (8 bit), w (16 bit), l (32 bit)
movl zmienna, %ebx
-
Adresowanie pamięci wykorzystuje () zamiast []
movl (%ebx), %eax
-
Adresowaniu skalowanemu w stylu Intela
[base + index*scale + disp]
w AT&T odpowiadadisp(base, index, scale)
np.movl %eax, -0xf4(%ebx, %ecx, 4)
Tutaj stałych nie należy poprzedzać znakiem $.
Do umieszczania prostych wstawek używamy instrukcji
asm( "Instrukcje asemblerowe");
Powoduje to proste wklejenie danego tekstu (kodu asemblerowego) do pliku generowanego przez gcc, bez żadnego sprawdzenia poprawności, np.
asm("movl %ecx, %eax \n\t addl %ebx, %eax");
Dlatego też konieczne jest np. wstawienie znaków nowej linii po każdej instrukcji.
Można też kolejne instrukcje oddzielać średnikiem i umieszczać je w osobnych łancuchach tekstowych.
asm("movl %ecx, %eax ;" "addl %ebx %eax;");
Jeżeli nasz kod modyfikuje jakiś rejestr i nie przywraca jego wartości może to prowadzić do błędnego działania programu. Kompilator (zwłaszcza podczas optymalizacji) może umieszczać pewne zmienne w rejestrach i zakładać, że one się nie zmienią.
Ogólna postać wstawki asemblerowej ma postać
asm ( "szablon instrukcji asemblerowych" : wyjściowe operandy /* optional */ : wejściowe operandy /* optional */ : lista niszczonych obiektów /* optional */ );
- Operandy podaje się jako listę oddzieloną przecinkami elementów postaci
"xxx" (wartosc)
gdzie xxx określa wymagania co do miejsca umieszczenia wartości np.- "a"(123) - wartość 123 ma być umieszczona w rejestrze eax
- "r"(dlugosc) - wartość zmiennej dlugosc ma być umieszczona w dowolnym rejestrze ogólnego przeznaczenia
- "m"(wysokosc) - wartość zmiennej wysokość ma być umieszczona w pamięci i przekazany będzie adres jej lokalizacji
- "i"(0xfffffc00) - wartość 0xfffffc00 będzie wstawiona do kodu jako argument instrukcji.
- Przed operandami wyjściowymi dodatkowo dajemy znak = np. "=r" (wyjscie)
- Operandy te są dostępne pod literałami %0, %1, %2, ... (liczy się najpierw wyjście potem wejście)
- % jest symbolem specjalnym dlatego nazwy rejestrów poprzedzamy dodatkowym % np. %%eax
- na wejściu wartość zmiennej x będzie w rejestrze eax, a zmienna y w ebx
- po zakończeniu wstawki wynik z rejestru eax kompilator umieści w zmiennej result
- x będzie w którymś z rejestrów dostępnym pod nazwą %1,
- y będzie w pamięci pod adresem %2
- wynik będzie zwrócony w rejestrze %0 i zapisany do zmiennej result,
- w ostatniej części informujemy kompilator, że nasz kod zmienia eax i kompilator nie może już ufać wartości tego rejestru, która wcześniej tam umieścił.
- 6 : Organizacja pamięci i dostęp do niej
- 11: Architektura pamięci i jej organizacja
- Prezentacja z wykładu
- Pamięć odwzorowywana bezpośrednio - szybka, prosta w implementacji,
wiersz z pamięci głównej zawsze trafia w to samo miejsce pamięci podręcznej
cześć adresu wystacza aby znaleźć wiersz w pamięci podręcznej np. bity 4-12. - Pamięć w pełni powiązana bardzo elastyczne, ale skomplikowane i wolne.
- Pamięć powiązana n-krotnie paczki po n wierszy,
procesor na podstawie adresu wybiera numer paczki (odwzorowanie bezpośrednie), ale wewnątrz paczki już pełne powiązanie
int x=2, y=3, result; asm( "addl %%ebx, %%eax" // : "=a"(result) // : "a"(x), "b"(y) // );
Ze względów optymalizacyjnych dobrze jest wybór rejestru do przekazywania parametrów pozostawić kompilatorowi, można też przekazywać zmienne w pamięci.
int x=2, y=3, result; asm( "movl %1, %%eax;" "addl %2, %%eax;" "movl %%eax, %0" : "=r"(result) : "r"(x), "m"(y) : "eax" );
Jeżeli chcemy zmodyfikować tylko zawartość rejestru bez niekoniecznego przepisywania jego wartości do rejestru wyjściowego, możemy powiązać rejestr wejściowy z wyjściowym. W tym celu w wymaganiach dla rejestru wejściowego podać numer rejestru wyjściowego np.
int x = 12345; asm("and %2, %0 \n\t" : "=r"(x) : "0"(x), "i"(0xffffff00) : );
Wynik
subq $16, %rsp # int x = 12345; movl $12345, -4(%rbp) movl -4(%rbp), %eax and $-256, %eax # wstawka movl %eax, -4(%rbp)
Jeżeli tak jak w kodzie poniżej używamy rejestrów wyjściowych do obliczeń mogą wystąpić problemy
int x=2, y=3, result; asm( "movl %1, %0;" "addl %2, %0;" : "=r"(result) : "r"(x), "r"(y) : );
Wyjściem jest poinformowanie kompilatora, że rejestr wyjściowy jest wcześnie nadpisywany i w takim razie nie powinien umieszczać w nim danych wejściowych. W tym celu używamy modyfikatora &
int x=2, y=3, result; asm( "movl %1, %0;" "addl %2, %0;" : "=&r"(result) : "r"(x), "r"(y) );
Należy nie nadużywać tego modyfikatora gdyż może to uniemożliwić optymalizację kodu.
; Rejestry ogólnego przeznaczenia "a" = eax, ax, al "b" = ebx, bx, bl "c" = ecx, cx, cl "d" = edx, dx, dl "S" = esi, si "D" = edi, di "A" = para rejestrów EDX:EAX (użyteczne np. przy zwracaniu 64 bitowych wyników) "r" = dowolny rejestr ogólnego przeznaczenia "q" = jeden z rejestrów a, b, c, d ; Adres pamięci "m" = zmienna w pamięci, operacje są wykonywane bezpośrednio na pamięci, powinno być używane gdy nie chcemy przechowywać wartości w rejestrze ; Rejestry zmiennoprzecinkowe "f" = dowolny rejestr zmiennoprzecinkowy "t" = ST0 "u" = ST1 ; Stałe "i" = stała całkowita, "I" = stała z zakresu 0..31 (dla przesunięć) "N" = stała z zakresu 0..255 "E" = stała zmiennoprzecinkowa
Wstawki można pisać w składni Intela. W tym celu należy we wstawce umieścić dyrektywę
.intel_syntax noprefix, a na końcu przywrócić składnię AT&T poprzez dyrektywę .att_syntax prefix
asm(".intel_syntax noprefix\n" "mov eax, ecx \n" "add eax, ebx \n" ".att_syntax prefix");
Obecnie odchodzi się od wstawek assemblerowych na rzecz funkcji wewnętrznych (intristic functions). Są to funkcje podobne do funkcji inline, zazwyczaj wykonujące konkretną operację assemblerową. The Intel Intrinsics Guide
Treści tego modułu zawarte są w książce Randall Hyde "Profesjonalne Programowanie, część 1: Zrozumieć komputer" w rozdziałach:
Tutaj umieszczam tylko listę tematów, które poruszyłem na wykładzie.
; ???
Np. 8 kB pamięci podręcznej może być podzielony na 512 bloków po 16 bajtów każdy.
Rozmiar cache można sprawdzić poleceniem (Linux):
sudo dmidecode -t cache
cat /proc/cpuinfoWięcej informacji znajduje się w folderze
/sys/devices/system/cpu/cpu0/cache/
; ???
; ???
Treści tego modułu zawarte są w książce Randall Hyde "Profesjonalne Programowanie, część 1: Zrozumieć komputer" w rozdziałach:
- 9 : Architektura procesora
- 10: Konstrukcja zbioru instrukcji
Tutaj umieszczam tylko listę tematów, które poruszyłem na wykładzie:
- CISC Complex Instruction Set Computers
- RISC Reduced Instruction Set Computers
- VLIW Very Long Instruction Word
Logika przypadku
- Instrukcja jest zakodowana na stałe w układzie (krzemie).
- Nie ma potrzeby czytania kodu z pamięci, co zwiększa szybkość.
- Im więcej instrukcji tym układ scalony staje się bardziej złożony i trudniejszy w modyfikacji.
Mikro kod
- Wewnętrznie znajduje się szybka jednostka z małą liczbą instrukcji wykonująca mikro kod z banku instrukcji.
- Instrukcje są czytane z pamięci ROM - ogranicza to szybkość.
- Łatwo jest dodać kolejne instrukcje lub zmodyfikować istniejące.
Obecne procesory wykorzystują obie techniki!
MOV DestReg, SrcReg
Kopiowanie wartości z rejestru SrcReg do rejestru DestReg.- Pobranie kodu instrukcji z pamięci
- Aktualizacja rejestru EIP (wskaźnik następnej instrukcji)
- Dekodowanie kodu instrukcji
- Pobranie danych z rejestru SrcReg
- Zapis wartości w DestReg
MOV [DestMem], SrcReg
Kopiowanie wartości z rejestru SrcReg do pamięci pod adres DestMem.- Pobranie kodu instrukcji z pamięci
- Aktualizacja rejestru EIP
- Dekodowanie kodu instrukcji
- Pobranie adresu znajdującego się za kodem instrukcji
- Aktualizacja rejestru EIP
- Wyliczenie adresu efektywnego (zależy od trybu)
- Pobranie danych z rejestru SrcReg
- Zapis wartości w [DestMem]
ADD DestReg, [Mem]
Dodawanie do wartości w rejestrze DestReg wartości z pamięci pod adresem Mem.- Pobranie kodu instrukcji z pamięci
- Aktualizacja rejestru EIP
- Dekodowanie kodu instrukcji
- Pobranie adresu znajdującego się za kodem instrukcji
- Aktualizacja rejestru EIP
- Wyliczenie adresu efektywnego (zależy od trybu)
- Pobranie danej z [Mem] i przeslanie do ALU
- Przesłanie wartości z rejestru DestReg do ALU
- Nakazanie ALU dodanie wartości
- Zapis wartości w DestReg
- Aktualizacja rejestru flag
ADD DestReg, [Mem]
Dodawanie do wartości w rejestrze DestReg wartości z pamięci pod adresem Mem.- Pobranie kodu instrukcji z pamięci
- Aktualizacja rejestru EIP
- Dekodowanie kodu instrukcji
- Pobranie adresu znajdującego się za kodem instrukcji
- Aktualizacja rejestru EIP
- Wyliczenie adresu efektywnego (zależy od trybu)
- Pobranie danej z [Mem] i przeslanie do ALU
- Przesłanie wartości z rejestru DestReg do ALU
- Nakazanie ALU dodanie wartości
- Zapis wartości w DestReg
- Aktualizacja rejestru flag
Niektóre kroki można wykonać jednocześnie.
Niestety większość kroków jest sekwencyjna.
Wydajność procesora można mierzyć średnią liczbą instrukcji wykonywanych na jeden cykl zegara (IPC - Instructions Per Clockcycle)
- IPC < 1 - komputery subskalarne
- IPC = 1 - komputery skalarne
- IPC > 1 - komputery superskalarne
Jeżeli instrukcje są wykonywane sekwencyjnie bardzo trudno jest uzyskać skalarność.
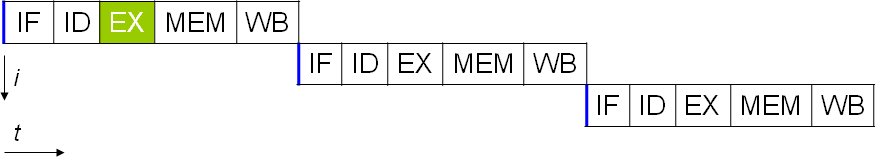
Modelowy 5-stopniowy potok 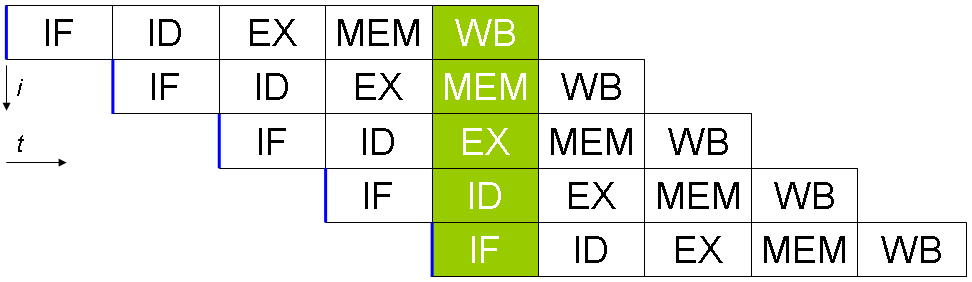
- Pobranie instrukcji z pamięci – ang. instruction fetch (IF)
- Zdekodowanie instrukcji – ang. instruction decode (ID)
- Wykonanie instrukcji – ang. execute (EX)
- Dostęp do pamięci – ang. memory access (MEM)
- Zapisanie wyników działania instrukcji – ang. store; write back (WB)
- Problem z dekodowaniem
instrukcje x86 mają od 1 do 15 bajtów długości.
Pod jakim adresem znajduje się następna instrukcja?
Rozwiązanie: Pobieranie spod kilku adresów i potem selekcja właściwego. - Zagrożenia (hazard) danych
kolejna instrukcja zależy do wyników zwracanych przez poprzednią instrukcję.mov rbx, tab mov eax, [rbx+4] add eax, 5 mov [rbx+4], eax
- Cały potok musi czekać na zakończenie pierwszej instrukcji.
- Długie ciągi zależności kolejnych instrukcji powodują, że w praktyce kolejne instrukcje są wykonywane sekwencyjnie zamiast równolegle.
- Może pomóc: zmiana kolejności instrukcji, zmiana wykorzystywanych rejestrów.
- Hazard RAW (read after write) i WAW (write after write).
- Zagrożenia sterowania
modyfikacje rejestru IP poprzez skoki, wywołania funkcji powoduje, że cały potok jest błędny (wstępnie przetworzone instrukcje zostały pobrane spod złego adresu) i należy go wyczyścić a następnie rozpocząć przetwarzanie instrukcji spod nowego adresu.- Powoduje to duże opóźnienia: pobranie instrukcji z pamieci + pierwsza instrukcja trwa tyle cykli ile potok ma kroków.
- Im dłuższy potok, tym dłuższe oczekiwanie.
- Pomaga odpowiednie pisanie instrukcji warunkowych, pętli, stosowanie funkcji inline.
- W procesorach implementowane jest spekulacyjne wykonanie kodu i przewidywanie rozgałęzień.
Wykorzystywane techniki:
- Zmiana kolejności wykonywania kodu.
- Zmiany nazw rejestrów
- Przewidywanie rozgałęzień, skoków.
- Powielenie jednostek wykonywania.
VLIW - Very Long Instruction Word
Jest to architektura, w której "instrukcje" VLIW są stałej długości i jest tak naprawdę zestawem kilku instrukcji.
___________________________________________ | INSTRUKCJA1 | INSTRUKCJA2 | INSTRUKCJA3 | -------------------------------------------To kompilator (programista) decyduje jakie instrukcje można spakować razem!
Procesor nie sprawdza ich niezależności.
Itanium2
- 128 bit VLIW = 3 instrukcje
- Można pobrać na raz dwa VLIW dlatego można wykonać do 6 instrukcji na cykl.
- 30 jednostek wykonania kodu:
- 6 x ALU, 2 x Integer, Shifts
- 4 x Data Cache
- 6 x Multimedia, 2 x Parallel Shifts, ...
- 2 x FMA, SIMD FMA
- 3 x Branch units.
- predykcjach i spekulatywnym wykonaniu kodu,
- przewidywaniu rozgałęzień,
- zmianach nazw rejestrów.
Mimo dużego entuzjazmu testy nie potwierdziły dużego wzrostu wydajności.
W 2004 roku komputer z Itanium2 był na drugim miejscu na liście TOP500.
| Przedrostek (0-4 bajtów) np. LOCK, REP, REPZ | |
| Kod instrukcji (1-2) bajty | |
| Bajt ModR/M - tryb adresowania, rejestry | |
| Bajt SIB (opcjonalny) - skala, index, baza | |
| Pole przesunięcia (opcjonalne) 0-4 bajtów | |
| Dane stałe (immediate, opcjonalne) 0-4 bajtów |
Online assembler & disassembler
- Łańcuch zależności jest to ciąg instrukcji, w którym wykonanie następnej instrukcji zależy od wyniku poprzedniej.
- Latency (opóźnienie) - dla instrukcji jest to opóźnienie jakie powoduje w łańcuchu zależnośći. Jest to w przybliżeniu liczba cykli zegara jakie potrzebuje CPU aby daną instrukcję wykonać. (Bardziej dokładnie ile musi czekać następna instrukcja która jest od niej zależna).
- Troughput (przepustowość) - jest to maksymalna liczba instrukcji tego samego rodzaju, która może być wykonana w jednym cyklu zegara (jeżeli nie ma między nimi zależności).
- Reciprocal throughput to odwrotność przepustowości. Jest to średnia liczba cykli zegara na instrukcje, które nie są częścią łańcucha zależnośći.
Więcej informacji można znaleźć w
- oficjalnych manualach AMD i Intela
- Software optimization resources
Wiele rzeczy może spowalniać pętle. Najprawdopodobniejsze wąskie gardła to
- Złe cache'owanie (częste nietrafienia w bufor)
- Propagowane przez pętle łańcuchy zależności
- Pobieranie instrukcji
- Decodowanie instrukcji
- Przepustowość portów
- Przepustowość jednostek wykonywania kodu
- Nieoptymalne kolejność wykonywania mikrooperacji
- Pomyłki w przewidywaniu rozgałęzień
- Wyjątki w obliczeniach zmiennoprzecinkowych i operacje na liczbach zdenormalizowanych
Należy znaleść wąskie gardło, które najbardziej ogranicza wydajność. Przeważnie poprawianie innych rzeczy nie daje żadnej poprawy.
Dzisiejsze komputery mają potoki, złożone z wielu etapów (od 12 do 22), dlatego bardzo ważne aby przy skokach, rozgałęzieniach czy wywołaniach funkcji nie trzeba było czekać na następną instrukcję do chwili gdy będzie wiadomo jaki jest jej adres.
Dlatego rozwijane są specjalne jednostki odpowiedzialne za przewidywanie, która z możliwych gałęzi zostanie wybrana. Obecnie używają one bardzo zaawansowanych algorytmów do przewidywania.
Pomyłka w przewidywaniu kosztuje od 12 do 50 cykli zegara.
Rozgałęzienia są przeważnie dobrze przewidywane w następujących przypadkach
- zawsze jest wybierana ta sama gałąź,
- gałęzie są wybierane według prostego wzoru wewnątrz pętli, która nie ma rozgałęzień lub ma ich niewiele,
- rozgałęzienie jest skorelowane z poprzedzającym je rozgałęzieniem,
- jeżeli rozgałęzienie jest pętlą o stałej, niewielkiej liczbie powtórzeń oraz w wewnątrz pętli nie ma zbyt wielu rozgałęzień
- Rozgałęzienia są słabo przewidywalne jeżeli każda z gałęzi jest wybierana średnio z częstotliwością 50% i nie ma prostej reguły wyboru ani skorelowania z poprzednimi rozgałęzieniami.
- Należy unikać dużej liczby rozgałęzień wewnątrz pętli. Czasami korzystniej jest podzielić jedną dużą pętlę na kilka mniejszych.
- Skoki pośrednie i pośrednie wywołania funkcji (gdzie adres skoku jest efektem pewnych obliczeń) są często słabo przewidywalne. Starsze procesory przewidują ze adres będzie ten sam co ostatnio, nowsze potrafią wykrywać proste wzorce.
- Powroty są przewidywane przez bufor przechowujący adresy powrotu dla ostatnio wywołanych funkcji.
Jeżeli ma on miejsce na 16 adresów to może poprawnie przewidywać powroty do 16 poziomu zagnieżdżenia. Jeżeli się przepełni to opóźnienia będą tylko dla najbardziej zewnętrznych funkcji (więc sporadyczne).
Bufor ten zawiedzie jeżeli wywołania CALL i RET nie są sparowane.
Spraw aby skoki warunkowe były rzadko wykonywane
cmp eax,567 je L1 ; częstsza gałąź ret L1: ; rzadko wykonywana gałąź ret
Jeżeli wywołanie funkcji jest bezpośrednio przed RET można zastąpić skokiem
Func1: ... call Func2 ret | Func1: ... jmp Func2 |
Należy pamiętać o wcześniejszym posprzątaniu stosu i ewentualnym odtworzeniu ebp.
Func1: enter 32 ... call Func2 leave ret | Func1: enter 32 ... leave jmp Func2 |
Funkcja: push ebp mov ebp, esp mov ecx, [iloscElementow] lea edx, [adresTablicy] mov eax, [wartoscProgowa] Loop1: ; początek pętli cmp eax, [edx+4*ecx-4] ; if-else ja ElseBranch ... ; pierwsza gałąź jmp EndIf ElseBranch: .... ; druga gałąź EndIf: sub ecx, 1 ; epilog pętli jnz Loop1 mov esp, ebp ; epilog funkcji pop ebp ret
Przez powielenie epilogu pętli mozemy wyeliminować skok do EndIf
Funkcja: push ebp mov ebp, esp mov ecx, [iloscElementow] lea edx, [adresTablicy] mov eax, [wartoscProgowa] Loop1: ; początek pętli cmp eax, [edx+4*ecx-4] ; if-else ja ElseBranch ... ; pierwsza gałąź sub ecx, 1 ; epilog pętli 1 jnz Loop1 jmp EndLoop ElseBranch: .... ; druga gałąź sub ecx, 1 ; epilog pętli 2 jnz Loop1 EndLoop: mov esp, ebp ; epilog funkcji pop ebp ret
Przez powielenie epilogu funkcji mozemy wyeliminować skok do EndLoop (tutaj zysk prędkości jest już niewielki).
Funkcja: push ebp mov ebp, esp mov ecx, [iloscElementow] lea edx, [adresTablicy] mov eax, [wartoscProgowa] Loop1: ; początek pętli cmp eax, [edx+4*ecx-4] ; if-else ja ElseBranch ... ; pierwsza gałąź sub ecx, 1 ; epilog pętli 1 jnz Loop1 mov esp, ebp ; epilog funkcji 1 pop ebp ret ElseBranch: .... ; druga gałąź sub ecx, 1 ; epilog pętli 2 jnz Loop1 mov esp, ebp ; epilog funkcji 2 pop ebp ret
Skoki warunkowe często mogą zostać wyeliminowane przy użyciu warunkowych CMOVxx. Instrukcja MOV zostanie wykonana tylko jeżeli spełniony jest warunek xx np. cmovb, cmovae, cmovnz, cmovle.
a = b > c ? d : e ;
mov eax, [b] cmp eax, [c] jng L1 mov eax, [d] jmp L2 L1: mov eax, [e] L2: mov [a], eax | mov eax, [b] cmp eax, [c] mov eax, [d] cmovng eax, [e] mov [a], eax |
- Ta metoda jest szczególnie skuteczna gdy skoki są błednie przewidywane.
- Minusem jest tworzenie długiego łańcucha zależności.
- Opóźnienie (latency) CMOVxx dla Intela to 2, dla AMD wynosi 1.
- Jeżeli d i e są rezultatem dłuższych obliczeń to przy wykorzystaniu CMOVxx to obie wartości muszą być obliczone. Przy zastosowaniu rozgałęzienia tylko jedna z nich.
- Zwłaszcza w pętlach CMOVxx może prowadzić do bardzo długich łańcuchów zależności obniżających szybkość kodu.
- Aby obliczyć minimum lub maksimum dwóch liczb można użyć jednostek wektorowych, które mają do tego celu specjalne instrukcje.
int b, c; bool a = b > c;
; wynik 8 - bitowy mov eax, [b] cmp eax, [c] setg al mov [a], al | ; wynik 32-bitowy mov eax, [b] ; zerujemy rejestr przed cmp ; aby uniknąć zmian flag xor ebx, ebx cmp eax, [c] setg bl mov [a], ebx |
Obliczanie wartości bezwzględnej
cdq ; wypełnia edx bitem znaku eax xor eax, edx ; odwraca bity jeżeli eax < 0 sub eax, edx ; dodaje 1 jeżeli eax < 0
Obliczanie minimum dwóch liczb bez znaku b = min (a , b)
sub eax, ebx ; = a-b sbb edx, edx ; = (b > a) ? 0xFFFFFFFF : 0 and edx, eax ; = (b > a) ? a-b : 0 add ebx, edx ; = (b > a) ? a : b
Zmniejszenie rozmiaru kodu może pomóc lepiej cache'ować instrukcje.
Decodowanie krótszego kodu jest szybsze.
Pętle krótsze niż 64 bajty wykonują się bardzo szybko na niektórych procesorach
Jeżeli na urządzeniu mamy ograniczoną pamięć a nie zależy nam na prędkości.
PUSH, POP, INC, DEC z rejestrami ogólnego przeznaczenia są jednobajtowe.
Instrukcje ADD, ADC, SUB, SBB, AND, OR, XOR, CMP, TEST, MOV zajmują jeden bajt mniej jeżeli są używane z rejestrem EAX.
Instrukcje po lewej są krótsze
add eax, 1000 mov eax, [mem] | add ebx, 1000 mov ebx, [mem] |
Przy skalowanym adresowaniu pewne kombinacje rejestrów, skalowań dają dłuższe instrukcje np.
Instrukcje po lewej są krótsze
mov eax, [array+ebx] mov eax, [ebx+12] mov eax, [ebx] lea eax, [ebx+ebx] | mov eax, [4*ebx] mov eax, [esp+12] mov eax, [ebp] lea eax, [2*ebx] |
Instrucje zmiennoprzecinkowe na FPU są krótsze niż odpowiadające im instrukcje na SSE
fadd st(0), st(1) ; 2 bytes addsd xmm0, xmm1 ; 4 bytes
Często aby zapisać stałą albo przesunięcie wystarcza jeden bajt. Dlatego jeżeli to możliwe dobrze jest używać bliskich skoków.
Użycie wskaźnika i jednobajtowego przesunięcia zamiast adresu.
mov ebx, [mem1] ; 6b add ebx, [mem2] ; 6b | mov eax, offset mem1 ; 5b mov ebx, [eax] ; 2b add ebx, [eax+(mem2-mem1)]; 3b |
Wiekszość instrukcji ze stałymi z zakresu od -128 do 127 są krótsze. Stałe są rozszerzane bitem znaku.
push 200 ; 5b push 100 ; 2b add ebx, 128 ; 6b add ebx, -128 ; 3b
Krótsze wersje dla inicjowania rejestru stałą
mov eax, 0 ; 5b sub eax, eax ; 2b mov eax, 1 ; 5 b sub eax, eax / inc eax ; 3 b push 1 / pop eax ; 3 b mov eax, -1 ; 5 b or eax, -1 ; 3 b
Zastąpienie stałych obliczeniami arytmetycznymi
mov [mem1], 200 ; 10 b mov [mem2], 201 ; 10 b mov eax, 100 ; 5 b mov ebx, 150 ; 5 b ; w sumie 30 bajtów | mov eax, 200 ; 5 b mov [mem1], eax ; 5 b inc eax ; 1 b mov [mem2], eax ; 5 b sub eax, 101 ; 3 b lea ebx, [eax+50] ; 3b ; w sumie 22 bajtów |
Czasy dosteępu do pamięci to w przybliżeniu
- cache L1 - 3 cykle
- cache L2 - dziesiątki cykli
- DRAM - setki cykli
- pamięc swap (na dysku) - ekstremalnie długi czas dostępu.
Zmiana kolejności indeksowania może spowodować, że kod działa nawet 10 razy szybciej z uwagi na lepsze wykorzystanie pamięci podręcznej
// zapis kolumnami int array[256][256]; for( i=0; i<256; ++i) for( j=0; j<256; ++j) array[j][i] = i*j;
// zapis wierszami - zgodnie z ułożeniem w pamięci int array[256][256]; for( i=0; i<256; ++i) for( j=0; j<256; ++j) array[i][j] = i*j;
Wybieraj instrukcję która ma mniejszy opcode i mniej operandów. Wtedy cache'owanie instrukcji i dekodowanie jest wydajniejsze.
Używaj zmiennych lokalnych zamiast globalnych
- przesunięcie jest 1 bajtowe zamiast 4 czy 8 bajtowego.
- uzyskujemy lokalność odwołań do danych.
Wyrównanie przyspiesza dostęp do pamięci.
Szczególnie ważne:
- dane są czytane tylko raz, a sąsiednie komórki nie są wykorzystywane,
- dane są zapisywane przez jedną instrukcję a potem od razu wczytywane,
- używa się instrukcji SSE
Stos powinien być wyrównany do granicy 16 bajtów przed wywołaniem funkcji
w większości systemów operacyjnych.
Dobrze jest tak ułożyć lokalne zmienne aby były wyrównane do odpowiednich granic.
Bezpośrednie wyrównanie stosu
funkcja: ; jeden argument na stosie (32-bit) push ebp mov ebp, esp sub esp, zmienneLokalne and esp, 0FFFFFFF0H ; wyrównanie do 16b mov eax, [ebp+8] ; kopiowanie movdqu xmm0,[eax] ; z niewyrównanej tablic movdqa [esp],xmm0 ; do wyrównanej zmiennej lokalnej call SomeOtherFunction ... mov esp, ebp pop ebp ret
Możemy tak dobrać rozmiar danych lokalnych aby stos pozostał wyrównany
funkcja: ; (32-bit) sub esp, 28 mov eax, [esp+32] movdqu xmm0,[eax] movdqa [esp],xmm0 call SomeOtherFunction ... add esp, 28 ret
Jeżeli odkładamy wcześniej jakieś rejestry na stos to musimy je też wliczyć.
W kodzie 64 bitowym adresy są 8 bajtowe.
funkcja: ; (64-bit) sub rsp, 24 mov rax, [rsp+32] movdqu xmm0,[rax] movdqa [rsp],xmm0 call SomeOtherFunction ... add rsp, 24 ret
Okazuje się, że dzieki superskalarności zamiast
push eax push ebx push ecx
sub esp, 12 mov eax, [esp+8] mov ebx, [esp+4] mov ecx, [esp]
sub esp, 12 mov eax, [esp+8] mov ebx, [esp+4] mov ecx, [esp]
Jeżeli dane są wykorzystywane wielokrotnie albo wykorzystujemy wielu danych z ciągłęgo obszaru dobrze jest wczesniej pobrać je do odpowiedniego poziomu pamięci podręcznej. Służą do tego instrukcje
PREFETCH0 mem ; załaduj do wszystkich poziomów cache PREFETCH1 mem ; załaduj do wszystich poziomów poza L1 PREFETCH2 mem ; ... poza L1 i L2
Używaj PREFETCH wewnątrz pętli. Rozwiń częściowo pętlę tak aby w jednej iteracji "zużyć" cały wiersz cache'u.
mov rbx, tab mov rcx, [n] .loop: PREFETCH [rbx + 16] add eax, [rbx] add ebx, [rbx+4] add dcx, [rbx+8] add esi, [rbx+12] add rbx, 16 sub rcx, 4 jg .loop
We współczesnych procesorach mechanizmy przewidywania rozgałęzień i wstępnego pobierania danych i kodu działają tak dobrze, że dają często lepsze rezultaty niż ręczna optymalizacja.
Nietrafienia w cache są szczególnie kosztowne przy zapisach. Cały wiersz musi zostać wczytany, zmodyfikowany i zapisany do pamięci. Jeżeli zapisujemy dane, które z dużym prawdopodobieństwem nie będą ponownie wczytywane można użyć instrukcji które pomijają cache (non-temporal write) MOVNTI, MOVNTQ, MOVNTDQ, MOVNTPD, MOVNTPS.
Instrukcje te są jednak dość kosztowne i dają zysk jeżeli zapisuje się blok pamięci większy niż połowa rozmiaru największego cache'a.
Najczęstszymi miejscami krytycznymi programów są pętle
Optymalizacja pojedynczej instrukcji daje duży zysk dopiero
gdy ta instrukcja jest powtarzana wielokrotnie np. w pętli.
Narzut pętli to instrukcje potrzebne do skoku do początku pętli i do sprawdzenia warunku stopu.
Typowa pętla
for (int i = 0; i < n; i++) { // (loop body) }
Kod bez optymalizacji
mov ecx, [n] xor eax, eax ; i = 0 LoopTop: cmp eax, ecx ; i < n jge LoopEnd ; wyjście gdy i >= n ; (loop body) add eax, 1 ; i++ jmp LoopTop ; skok do początku LoopEnd:
Redukcja jednego skoku przez przesunięcie warunku na koniec
mov ecx, [n] test ecx, ecx jng LoopEnd ; opuść gdy n <= 0 xor eax, eax ; i = 0 LoopTop: ; (loop body) add eax, 1 ; i++ cmp eax, ecx ; i < n jl LoopTop ; kontynuuj jeżeli i < n LoopEnd:
Jeżeli nie potrzebujemy indeksu wewnątrz pętli możemy pozbyć się cmp odliczając w dół
mov ecx, [n] test ecx, ecx jng LoopEnd ; opuść gdy n <= 0 LoopTop: ; (loop body) sub ecx, 1 ; n-- jnz LoopTop ; kontynuuj jeżeli n!=0 LoopEnd:
Iterowanie od tyłu po tablicy jest nieoptymalne bo cache'owanie działa lepiej do przodu na a nie wstecz. Można to osiągnąć indeksując relatywnie do końca tablicy wartościami i = -n .. 1
mov ecx, [n] ; liczba elementów lea esi, [Array+4*ecx] ; wskaźnik na zaostatni element neg ecx ; i = -n jnl LoopEnd ; pomiń jeżeli (-n) >= 0 LoopTop: ; (Loop body) : dodajemy jeden do każdego elementu add dword [esi+4*ecx], 1 add ecx, 1 ; i++ js LoopTop ; powtorz jezeli i < 0 LoopEnd:
Strona 95.
We współczesnym programowaniu kładzie się nacisk na obiektowe orientowanie, modularność, wielokrotne wykorzystanie kodu, bezpieczeństwo.
Zaleca się aby funkcje nie były dłuższe niż kilka linii aby było łatwo je testować i utrzymać.
To często utrudnia optymalizację kodu ze względu na szybkość czy rozmiar.
Nie ma znaczącej różnicy w szybkości pomiędzy 32 a 64 bitowymi systemami.
64 bitowe systemy :
- mogą przyspieszyć 5-10% programy obliczeniowe z dużą liczbą wywołań funkcji (parametry w rejestrach a nie na stosie).
- więcej rejestrów
- Można zaadresować więcej niż 4GB danych.
Windows i Linux w 32-bitach używają tej samej konwencji więc wydajność jest zbliżona.
Mac OS X (na procesorach Intela) może być trochę wolniejszy bo używa domyślnie adresowania relatywnego i późnego łączenia.
Wybór języka programowania:
- kompilowane: C, C++, D, Pascal, Fortran
najszybsze, duża optymalizacja, - z kodem pośrednim: Java, C#
przenośność, bezpieczeństwo, możliwość optymalizacji na konkretną platformę - interpretowna z kompilacją just-in-time: Perl, Python
- interpretowane: JavaScript, PHP
Wybór kompilatora C++:
- Microsoft Visual Studio (tylko Windows, dobre IDE)
- Intel C++ compiler (bardzo dobrze optymalizuje, kod może nie działać na AMD)
- Gnu C++ Compiler (bardzo dobrze optymalizuje, dostępny na wiele platform,
- Clang (kompatybilny z GCC, następca GCC, czytelniejsze informacje o błędach)
Wybór bibliotek standardowych: Optimizing software in C++ strona 13.
GCC: -fno-builtin znacznie przyspiesza (zamiast wbudowanego kodu używa wersji bibliotecznych)
Aby znaleźć "wąskie gardło" programu można posłużyć się profilerem.
Większość kompilatorów ma swoje profilery. Istnieją też zewnętrzne np. AQtime, Intel VTune, AMD CodeXL, AMD CodeAnalyst.
Rodzaje profilerów:
- Instrumentacja - kompilator dodaje kawałek kodu do każdej funkcji, który zlicza liczbę wywołań, czas wykonania itd.
- Debugging - profiler dodaje breakpoint w każdej funkcji lub nawet w każdej linii i mierzy czasy wykonania.
- Time based sampling - system operacyjny generuje przerwania np. co milisekundę a profiler sprawdza w jakiej funkcji znajduje się wtedy program. Nie wymaga to zmian w programie ale jest mniej wiarygodne.
- Event-based sampling - profiler ustawia generowanie przerwań gdy nastąpi jakieś zdarzenie np. co każde 1000 nietrafień w bufor, złe przewidzenie rozgałezienia, rzucenie wyjątku.
Czasami najlepsze rezultaty daje własnoręczne dodanie liczników do wybranych funkcji czy miejsc.
Częste problemy z pofilerami:
- Za mała dokładność pomiaru czasu,
- Zbyt krótki lub zbyt długi czas wykonania (za mało lub za dużo danych do analizy),
- Czekanie na odpowiedź użytkownika lub innych komputerów (testować na przygotowanych danych z pliku)
- Zbyt duża optymalizacja może uniemożliwić rozpoznawanie wykonywanych funkcji (fałszywe raporty),
- Testowanie wersji debug, która nie jest zoptymalizowana,
- Skoki pomiędzy rdzeniami (można przypisać wątek do danego rdzenia),
- Mała powtarzalność (opóźnienia związane z przełączaniem zadań, garbage collection).
Przykład : test_gprof.c test_gprof_new.c (Pokaż/ukryj kod)
//test_gprof.c // gcc -Wall -pg test_gprof.c test_gprof_new.c -o test_gprof #include<stdio.h> void new_func1(void); void func1(void) { printf("\n Inside func1 \n"); int i = 0; for(;i<0x1fffffff;i++); new_func1(); } static void func2(void) { printf("\n Inside func2 \n"); int i = 0; for(;i<0x2fffffaa;i++); } int main(void) { printf("\n Inside main()\n"); int i = 0; for(;i<0xffffff;i++); func1(); func2(); func1(); return 0; }
//test_gprof.c // gcc -Wall -pg test_gprof.c test_gprof_new.c -o test_gprof #include<stdio.h> void new_func1(void); void func1(void) { printf("\n Inside func1 \n"); int i = 0; for(;i<0x1fffffff;i++); new_func1(); } static void func2(void) { printf("\n Inside func2 \n"); int i = 0; for(;i<0x2fffffaa;i++); } int main(void) { printf("\n Inside main()\n"); int i = 0; for(;i<0xffffff;i++); func1(); func2(); func1(); return 0; }
//test_gprof_new.c #include<stdio.h> void new_func1(void) { printf("\n Inside new_func1()\n"); int i = 0; for(;i<0x1fffffee;i++); }
Krok 1: Kompilujemy i linkujemy z opcją -pg
gcc -Wall -pg test_gprof.c test_gprof_new.c \
-o test_gprof
Krok 2: Wykonujemy kod
./test_gprofTo wygeneruje informacje do pliku gmon.out w bieżącym katalogu.
Krok 3: Analizujemy informacje używając gprof
gprof test_gprof gmon.out > analysis.txtParametrami są program który profilujemy oraz plik z wygenerowanymi informacjami.
Plik analysis.txt zawiera zestawienie funkcji posortowanych względem sumarycznego czasu wykonania oraz graf wywołań (która funkcja wywoływała daną funkcję i ile razy).
Profilowanie tylko wybranych funkcji
Tylko wybrane pliki kompilujemy z opcją -pg
gcc -Wall -pg -c test_gprof.c -o test2_gprof.o gcc -Wall -c test_gprof_new.c -o test2_gprof_new.o gcc -Wall -pg test2_gprof.o test2_gprof_new.o -o test2
Po uruchomieniu i analizie gprof otrzymujemy plik plik.
Podobny efekt otrzymamy dla funkcji bibliotecznych.
Biblioteka linpack służy do obliczeń numerycznych, dostarcza bardzo wydajnych algorytmów algebry liniowej zooptymalizowanych dla danego systemu i procesora.
Wygenerujemy raport dla jednego z testów wydajnościowych:
- linpack_bench.cpp (Pokaż/ukryj kod)
# include <cstdlib> # include <iostream> # include <iomanip> # include <cmath> # include <ctime> using namespace std; int main ( void ); double cpu_time ( void ); double r8_abs ( double x ); double r8_epsilon ( void ); double *r8_matgen ( int lda, int n ); double r8_max ( double x, double y ); double r8_random ( int iseed[4] ); void daxpy ( int n, double da, double dx[], int incx, double dy[], int incy ); double ddot ( int n, double dx[], int incx, double dy[], int incy ); int dgefa ( double a[], int lda, int n, int ipvt[] ); void dgesl ( double a[], int lda, int n, int ipvt[], double b[], int job ); void dscal ( int n, double sa, double x[], int incx ); int idamax ( int n, double dx[], int incx ); void timestamp ( void ); //****************************************************************************80 int main ( void ) //****************************************************************************80 // // Purpose: // // LINPACK_BENCH drives the double precision LINPACK benchmark program. // { # define N 1000 # define LDA ( N + 1 ) double *a; double a_max; double *b; double b_max; double cray = 0.056; double eps; int i; int info; int *ipvt; int j; int job; double ops; double *resid; double resid_max; double residn; double *rhs; double t1; double t2; double time[6]; double total; double *x; // // This program was updated on 10/12/92 to correct a // problem with the random number generator. The previous // random number generator had a short period and produced // singular matrices occasionally. // timestamp ( ); cout << "\n"; cout << "LINPACK_BENCH\n"; cout << " The LINPACK benchmark.\n"; cout << " Language: C++\n"; cout << " Datatype: Double\n"; ops = ( double ) ( 2 * N * N * N ) / 3.0 + 2.0 * ( double ) ( N * N ); a = r8_matgen ( LDA, N ); b = new double[N]; ipvt = new int[N]; resid = new double[N]; rhs = new double[N]; x = new double[N]; a_max = 0.0; for ( j = 1; j <= N; j++ ) { for ( i = 1; i <= N; i++ ) { a_max = r8_max ( a_max, a[i-1+(j-1)*LDA] ); } } for ( i = 1; i <= N; i++ ) { x[i-1] = 1.0; } for ( i = 1; i <= N; i++ ) { b[i-1] = 0.0; for ( j = 1; j <= N; j++ ) { b[i-1] = b[i-1] + a[i-1+(j-1)*LDA] * x[j-1]; } } // // DEBUG: // b_max = 0.0; for ( i = 1; i <= N; i++ ) { b_max = r8_max ( b_max, r8_abs ( b[i-1] ) ); } t1 = cpu_time ( ); info = dgefa ( a, LDA, N, ipvt ); if ( info != 0 ) { cout << "\n"; cout << "LINPACK_BENCH - Fatal error!\n"; cout << " The matrix A is apparently singular.\n"; cout << " Abnormal end of execution.\n"; return 1; } t2 = cpu_time ( ); time[0] = t2 - t1; t1 = cpu_time ( ); job = 0; dgesl ( a, LDA, N, ipvt, b, job ); t2 = cpu_time ( ); time[1] = t2 - t1; total = time[0] + time[1]; delete [] a; // // Compute a residual to verify results. // a = r8_matgen ( LDA, N ); for ( i = 1; i <= N; i++ ) { x[i-1] = 1.0; } for ( i = 1; i <= N; i++ ) { rhs[i-1] = 0.0; for ( j = 1; j <= N; j++ ) { rhs[i-1] = rhs[i-1] + a[i-1+(j-1)*LDA] * x[j-1]; } } for ( i = 1; i <= N; i++ ) { resid[i-1] = -rhs[i-1]; for ( j = 1; j <= N; j++ ) { resid[i-1] = resid[i-1] + a[i-1+(j-1)*LDA] * b[j-1]; } } resid_max = 0.0; for ( i = 1; i <= N; i++ ) { resid_max = r8_max ( resid_max, r8_abs ( resid[i-1] ) ); } b_max = 0.0; for ( i = 1; i <= N; i++ ) { b_max = r8_max ( b_max, r8_abs ( b[i-1] ) ); } eps = r8_epsilon ( ); residn = resid_max / ( ( double ) N * a_max * b_max * eps ); time[2] = total; if ( 0.0 < total ) { time[3] = ops / ( 1.0E+06 * total ); } else { time[3] = -1.0; } time[4] = 2.0 / time[3]; time[5] = total / cray; cout << "\n"; cout << " Norm. Resid Resid MACHEP X[1] X[N]\n"; cout << "\n"; cout << setw(14) << residn << " " << setw(14) << resid_max << " " << setw(14) << eps << " " << setw(14) << b[0] << " " << setw(14) << b[N-1] << "\n"; cout << "\n"; cout << " Times are reported for matrices of order N = " << N << "\n"; cout << " with leading array dimension of LDA = " << LDA << "\n"; cout << "\n"; cout << " Factor Solve Total MFLOPS Unit Ratio\n"; cout << "\n"; cout << setw(9) << time[0] << " " << setw(9) << time[1] << " " << setw(9) << time[2] << " " << setw(9) << time[3] << " " << setw(9) << time[4] << " " << setw(9) << time[5] << "\n"; cout << "\n"; cout << " End of tests -- This version dated 10/12/92.\n"; delete [] a; delete [] b; delete [] ipvt; delete [] resid; delete [] rhs; delete [] x; cout << "\n"; cout << "LINPACK_BENCH\n"; cout << " Normal end of execution.\n"; cout << "\n"; timestamp ( ); return 0; # undef LDA # undef N } //****************************************************************************80 double cpu_time ( void ) //****************************************************************************80 // // Purpose: // // CPU_TIME returns the current reading on the CPU clock. // // Modified: // // 06 June 2005 // // Author: // // John Burkardt // // Parameters: // // Output, double CPU_TIME, the current reading of the CPU clock, in seconds. // { double value; value = ( double ) ( clock ( ) / CLOCKS_PER_SEC ); return value; } //****************************************************************************80 double r8_abs ( double x ) //****************************************************************************80 // // Purpose: // // R8_ABS returns the absolute value of a double precision number. // // Modified: // // 02 April 2005 // // Author: // // John Burkardt // // Parameters: // // Input, double X, the quantity whose absolute value is desired. // // Output, double R8_ABS, the absolute value of X. // { if ( 0.0 <= x ) { return x; } else { return ( -x ); } } //****************************************************************************80 double r8_epsilon ( void ) //****************************************************************************80 // // Purpose: // // R8_EPSILON returns the round off unit for double precision arithmetic. // // Discussion: // // R8_EPSILON is a number R which is a power of 2 with the property that, // to the precision of the computer's arithmetic, // 1 < 1 + R // but // 1 = ( 1 + R / 2 ) // // Modified: // // 01 July 2004 // // Author: // // John Burkardt // // Parameters: // // Output, double R8_EPSILON, the double precision round-off unit. // { double r; r = 1.0E+00; while ( 1.0E+00 < ( double ) ( 1.0E+00 + r ) ) { r = r / 2.0E+00; } return ( 2.0E+00 * r ); } //****************************************************************************80 double *r8_matgen ( int lda, int n ) //****************************************************************************80 // // Purpose: // // R8_MATGEN generates a random matrix. // // Modified: // // 06 June 2005 // // Parameters: // // Input, integer LDA, the leading dimension of the matrix. // // Input, integer N, the order of the matrix. // // Output, double R8_MATGEN[LDA*N], the N by N matrix. // { double *a; int i; int init[4] = { 1, 2, 3, 1325 }; int j; a = new double[lda*n]; for ( j = 1; j <= n; j++ ) { for ( i = 1; i <= n; i++ ) { a[i-1+(j-1)*lda] = r8_random ( init ) - 0.5; } } return a; } //****************************************************************************80 double r8_max ( double x, double y ) //****************************************************************************80 // // Purpose: // // R8_MAX returns the maximum of two double precision values. // // Modified: // // 18 August 2004 // // Author: // // John Burkardt // // Parameters: // // Input, double X, Y, the quantities to compare. // // Output, double R8_MAX, the maximum of X and Y. // { if ( y < x ) { return x; } else { return y; } } //****************************************************************************80 double r8_random ( int iseed[4] ) //****************************************************************************80 // // Purpose: // // R8_RANDOM returns a uniformly distributed random number between 0 and 1. // // Discussion: // // This routine uses a multiplicative congruential method with modulus // 2**48 and multiplier 33952834046453 (see G.S.Fishman, // 'Multiplicative congruential random number generators with modulus // 2**b: an exhaustive analysis for b = 32 and a partial analysis for // b = 48', Math. Comp. 189, pp 331-344, 1990). // // 48-bit integers are stored in 4 integer array elements with 12 bits // per element. Hence the routine is portable across machines with // integers of 32 bits or more. // // Parameters: // // Input/output, integer ISEED(4). // On entry, the seed of the random number generator; the array // elements must be between 0 and 4095, and ISEED(4) must be odd. // On exit, the seed is updated. // // Output, double R8_RANDOM, the next pseudorandom number. // { int ipw2 = 4096; int it1; int it2; int it3; int it4; int m1 = 494; int m2 = 322; int m3 = 2508; int m4 = 2549; double one = 1.0; double r = 1.0 / 4096.0; double value; // // Multiply the seed by the multiplier modulo 2**48. // it4 = iseed[3] * m4; it3 = it4 / ipw2; it4 = it4 - ipw2 * it3; it3 = it3 + iseed[2] * m4 + iseed[3] * m3; it2 = it3 / ipw2; it3 = it3 - ipw2 * it2; it2 = it2 + iseed[1] * m4 + iseed[2] * m3 + iseed[3] * m2; it1 = it2 / ipw2; it2 = it2 - ipw2 * it1; it1 = it1 + iseed[0] * m4 + iseed[1] * m3 + iseed[2] * m2 + iseed[3] * m1; it1 = ( it1 % ipw2 ); // // Return updated seed // iseed[0] = it1; iseed[1] = it2; iseed[2] = it3; iseed[3] = it4; // // Convert 48-bit integer to a real number in the interval (0,1) // value = r * ( ( double ) ( it1 ) + r * ( ( double ) ( it2 ) + r * ( ( double ) ( it3 ) + r * ( ( double ) ( it4 ) ) ) ) ); return value; } //****************************************************************************80 void daxpy ( int n, double da, double dx[], int incx, double dy[], int incy ) //****************************************************************************80 // // Purpose: // // DAXPY computes constant times a vector plus a vector. // // Discussion: // // This routine uses unrolled loops for increments equal to one. // // Modified: // // 02 May 2005 // // Author: // // Jack Dongarra // // Reference: // // Dongarra, Moler, Bunch, Stewart, // LINPACK User's Guide, // SIAM, 1979. // // Lawson, Hanson, Kincaid, Krogh, // Basic Linear Algebra Subprograms for Fortran Usage, // Algorithm 539, // ACM Transactions on Mathematical Software, // Volume 5, Number 3, September 1979, pages 308-323. // // Parameters: // // Input, int N, the number of elements in DX and DY. // // Input, double DA, the multiplier of DX. // // Input, double DX[*], the first vector. // // Input, int INCX, the increment between successive entries of DX. // // Input/output, double DY[*], the second vector. // On output, DY[*] has been replaced by DY[*] + DA * DX[*]. // // Input, int INCY, the increment between successive entries of DY. // { int i; int ix; int iy; int m; if ( n <= 0 ) { return; } if ( da == 0.0 ) { return; } // // Code for unequal increments or equal increments // not equal to 1. // if ( incx != 1 || incy != 1 ) { if ( 0 <= incx ) { ix = 0; } else { ix = ( - n + 1 ) * incx; } if ( 0 <= incy ) { iy = 0; } else { iy = ( - n + 1 ) * incy; } for ( i = 0; i < n; i++ ) { dy[iy] = dy[iy] + da * dx[ix]; ix = ix + incx; iy = iy + incy; } } // // Code for both increments equal to 1. // else { m = n % 4; for ( i = 0; i < m; i++ ) { dy[i] = dy[i] + da * dx[i]; } for ( i = m; i < n; i = i + 4 ) { dy[i ] = dy[i ] + da * dx[i ]; dy[i+1] = dy[i+1] + da * dx[i+1]; dy[i+2] = dy[i+2] + da * dx[i+2]; dy[i+3] = dy[i+3] + da * dx[i+3]; } } return; } //****************************************************************************80 double ddot ( int n, double dx[], int incx, double dy[], int incy ) //****************************************************************************80 // // Purpose: // // DDOT forms the dot product of two vectors. // // Discussion: // // This routine uses unrolled loops for increments equal to one. // // Modified: // // 02 May 2005 // // Author: // // Jack Dongarra // // Reference: // // Dongarra, Moler, Bunch, Stewart, // LINPACK User's Guide, // SIAM, 1979. // // Lawson, Hanson, Kincaid, Krogh, // Basic Linear Algebra Subprograms for Fortran Usage, // Algorithm 539, // ACM Transactions on Mathematical Software, // Volume 5, Number 3, September 1979, pages 308-323. // // Parameters: // // Input, int N, the number of entries in the vectors. // // Input, double DX[*], the first vector. // // Input, int INCX, the increment between successive entries in DX. // // Input, double DY[*], the second vector. // // Input, int INCY, the increment between successive entries in DY. // // Output, double DDOT, the sum of the product of the corresponding // entries of DX and DY. // { double dtemp; int i; int ix; int iy; int m; dtemp = 0.0; if ( n <= 0 ) { return dtemp; } // // Code for unequal increments or equal increments // not equal to 1. // if ( incx != 1 || incy != 1 ) { if ( 0 <= incx ) { ix = 0; } else { ix = ( - n + 1 ) * incx; } if ( 0 <= incy ) { iy = 0; } else { iy = ( - n + 1 ) * incy; } for ( i = 0; i < n; i++ ) { dtemp = dtemp + dx[ix] * dy[iy]; ix = ix + incx; iy = iy + incy; } } // // Code for both increments equal to 1. // else { m = n % 5; for ( i = 0; i < m; i++ ) { dtemp = dtemp + dx[i] * dy[i]; } for ( i = m; i < n; i = i + 5 ) { dtemp = dtemp + dx[i ] * dy[i ] + dx[i+1] * dy[i+1] + dx[i+2] * dy[i+2] + dx[i+3] * dy[i+3] + dx[i+4] * dy[i+4]; } } return dtemp; } //****************************************************************************80 int dgefa ( double a[], int lda, int n, int ipvt[] ) //****************************************************************************80 // // Purpose: // // DGEFA factors a real general matrix. // // Modified: // // 16 May 2005 // // Author: // // C++ translation by John Burkardt. // // Reference: // // Dongarra, Moler, Bunch and Stewart, // LINPACK User's Guide, // SIAM, (Society for Industrial and Applied Mathematics), // 3600 University City Science Center, // Philadelphia, PA, 19104-2688. // ISBN 0-89871-172-X // // Parameters: // // Input/output, double A[LDA*N]. // On intput, the matrix to be factored. // On output, an upper triangular matrix and the multipliers used to obtain // it. The factorization can be written A=L*U, where L is a product of // permutation and unit lower triangular matrices, and U is upper triangular. // // Input, int LDA, the leading dimension of A. // // Input, int N, the order of the matrix A. // // Output, int IPVT[N], the pivot indices. // // Output, int DGEFA, singularity indicator. // 0, normal value. // K, if U(K,K) == 0. This is not an error condition for this subroutine, // but it does indicate that DGESL or DGEDI will divide by zero if called. // Use RCOND in DGECO for a reliable indication of singularity. // { int info; int j; int k; int l; double t; // // Gaussian elimination with partial pivoting. // info = 0; for ( k = 1; k <= n-1; k++ ) { // // Find L = pivot index. // l = idamax ( n-k+1, a+(k-1)+(k-1)*lda, 1 ) + k - 1; ipvt[k-1] = l; // // Zero pivot implies this column already triangularized. // if ( a[l-1+(k-1)*lda] == 0.0 ) { info = k; continue; } // // Interchange if necessary. // if ( l != k ) { t = a[l-1+(k-1)*lda]; a[l-1+(k-1)*lda] = a[k-1+(k-1)*lda]; a[k-1+(k-1)*lda] = t; } // // Compute multipliers. // t = -1.0 / a[k-1+(k-1)*lda]; dscal ( n-k, t, a+k+(k-1)*lda, 1 ); // // Row elimination with column indexing. // for ( j = k+1; j <= n; j++ ) { t = a[l-1+(j-1)*lda]; if ( l != k ) { a[l-1+(j-1)*lda] = a[k-1+(j-1)*lda]; a[k-1+(j-1)*lda] = t; } daxpy ( n-k, t, a+k+(k-1)*lda, 1, a+k+(j-1)*lda, 1 ); } } ipvt[n-1] = n; if ( a[n-1+(n-1)*lda] == 0.0 ) { info = n; } return info; } //****************************************************************************80 void dgesl ( double a[], int lda, int n, int ipvt[], double b[], int job ) //****************************************************************************80 // // Purpose: // // DGESL solves a real general linear system A * X = B. // // Discussion: // // DGESL can solve either of the systems A * X = B or A' * X = B. // // The system matrix must have been factored by DGECO or DGEFA. // // A division by zero will occur if the input factor contains a // zero on the diagonal. Technically this indicates singularity // but it is often caused by improper arguments or improper // setting of LDA. It will not occur if the subroutines are // called correctly and if DGECO has set 0.0 < RCOND // or DGEFA has set INFO == 0. // // Modified: // // 16 May 2005 // // Author: // // C++ translation by John Burkardt. // // Reference: // // Dongarra, Moler, Bunch and Stewart, // LINPACK User's Guide, // SIAM, (Society for Industrial and Applied Mathematics), // 3600 University City Science Center, // Philadelphia, PA, 19104-2688. // ISBN 0-89871-172-X // // Parameters: // // Input, double A[LDA*N], the output from DGECO or DGEFA. // // Input, int LDA, the leading dimension of A. // // Input, int N, the order of the matrix A. // // Input, int IPVT[N], the pivot vector from DGECO or DGEFA. // // Input/output, double B[N]. // On input, the right hand side vector. // On output, the solution vector. // // Input, int JOB. // 0, solve A * X = B; // nonzero, solve A' * X = B. // { int k; int l; double t; // // Solve A * X = B. // if ( job == 0 ) { for ( k = 1; k <= n-1; k++ ) { l = ipvt[k-1]; t = b[l-1]; if ( l != k ) { b[l-1] = b[k-1]; b[k-1] = t; } daxpy ( n-k, t, a+k+(k-1)*lda, 1, b+k, 1 ); } for ( k = n; 1 <= k; k-- ) { b[k-1] = b[k-1] / a[k-1+(k-1)*lda]; t = -b[k-1]; daxpy ( k-1, t, a+0+(k-1)*lda, 1, b, 1 ); } } // // Solve A' * X = B. // else { for ( k = 1; k <= n; k++ ) { t = ddot ( k-1, a+0+(k-1)*lda, 1, b, 1 ); b[k-1] = ( b[k-1] - t ) / a[k-1+(k-1)*lda]; } for ( k = n-1; 1 <= k; k-- ) { b[k-1] = b[k-1] + ddot ( n-k, a+k+(k-1)*lda, 1, b+k, 1 ); l = ipvt[k-1]; if ( l != k ) { t = b[l-1]; b[l-1] = b[k-1]; b[k-1] = t; } } } return; } //****************************************************************************80 void dscal ( int n, double sa, double x[], int incx ) //****************************************************************************80 // // Purpose: // // DSCAL scales a vector by a constant. // // Modified: // // 02 May 2005 // // Author: // // Jack Dongarra // // Reference: // // Dongarra, Moler, Bunch, Stewart, // LINPACK User's Guide, // SIAM, 1979. // // Lawson, Hanson, Kincaid, Krogh, // Basic Linear Algebra Subprograms for Fortran Usage, // Algorithm 539, // ACM Transactions on Mathematical Software, // Volume 5, Number 3, September 1979, pages 308-323. // // Parameters: // // Input, int N, the number of entries in the vector. // // Input, double SA, the multiplier. // // Input/output, double X[*], the vector to be scaled. // // Input, int INCX, the increment between successive entries of X. // { int i; int ix; int m; if ( n <= 0 ) { } else if ( incx == 1 ) { m = n % 5; for ( i = 0; i < m; i++ ) { x[i] = sa * x[i]; } for ( i = m; i < n; i = i + 5 ) { x[i] = sa * x[i]; x[i+1] = sa * x[i+1]; x[i+2] = sa * x[i+2]; x[i+3] = sa * x[i+3]; x[i+4] = sa * x[i+4]; } } else { if ( 0 <= incx ) { ix = 0; } else { ix = ( - n + 1 ) * incx; } for ( i = 0; i < n; i++ ) { x[ix] = sa * x[ix]; ix = ix + incx; } } return; } //****************************************************************************80 int idamax ( int n, double dx[], int incx ) //****************************************************************************80 // // Purpose: // // IDAMAX finds the index of the vector element of maximum absolute value. // // Modified: // // 02 May 2005 // // Reference: // // Dongarra, Moler, Bunch, Stewart, // LINPACK User's Guide, // SIAM, 1979. // // Lawson, Hanson, Kincaid, Krogh, // Basic Linear Algebra Subprograms for Fortran Usage, // Algorithm 539, // ACM Transactions on Mathematical Software, // Volume 5, Number 3, September 1979, pages 308-323. // // Parameters: // // Input, int N, the number of entries in the vector. // // Input, double X[*], the vector to be examined. // // Input, int INCX, the increment between successive entries of SX. // // Output, int IDAMAX, the index of the element of maximum // absolute value. // { double dmax; int i; int ix; int value; value = 0; if ( n < 1 || incx <= 0 ) { return value; } value = 1; if ( n == 1 ) { return value; } if ( incx == 1 ) { dmax = r8_abs ( dx[0] ); for ( i = 1; i < n; i++ ) { if ( dmax < r8_abs ( dx[i] ) ) { value = i + 1; dmax = r8_abs ( dx[i] ); } } } else { ix = 0; dmax = r8_abs ( dx[0] ); ix = ix + incx; for ( i = 1; i < n; i++ ) { if ( dmax < r8_abs ( dx[ix] ) ) { value = i + 1; dmax = r8_abs ( dx[ix] ); } ix = ix + incx; } } return value; } //****************************************************************************80 void timestamp ( void ) //****************************************************************************80 // // Purpose: // // TIMESTAMP prints the current YMDHMS date as a time stamp. // // Example: // // May 31 2001 09:45:54 AM // // Modified: // // 24 September 2003 // // Author: // // John Burkardt // // Parameters: // // None // { # define TIME_SIZE 40 static char time_buffer[TIME_SIZE]; const struct tm *tm; size_t len; time_t now; now = time ( NULL ); tm = localtime ( &now ); len = strftime ( time_buffer, TIME_SIZE, "%d %B %Y %I:%M:%S %p", tm ); cout << time_buffer << "\n"; return; # undef TIME_SIZE }
- skrypt generujący raport
- raport
Przed przystąpieniem do optymalizacji kodu należy ustalić gdzie naprawdę znajduje się krytyczne miejsce. Często problem nie leży w wydajności operacji ale np.
- proces instalacji
- automatyczne uaktualnienia np. przy każdym uruchomieniu,
- długi czas ładowania się programu (duże frameworki np. Java, C#, dużo dynamicznie ładowanych bibliotek zewnętrznych)
- dostęp do plików
- dostęp do baz danych
- graficzny interfejs użytkownika
- dostęp do sieci i zdalnych zasobów
- dostęp do pamięci, cache'owanie
- przełączanie pomiędzy różnymi wątkami czy zadaniami
- łańcuchy zależności kolejnych instrukcji
- przepustowość jednostek wykonywania kodu
#include <iostream> #include <cstdio> #include <time.h> #include <cstdlib> using namespace std; // Example 9.9a const int SIZE = 512; // number of rows/columns in matrix //const int SIZE = 513; // number of rows/columns in matrix const int liczba_powtorzen = 2000; void transpose(double a[SIZE][SIZE]) { // function to transpose matrix // define a macro to swap two array elements: #define swapd(x,y) {temp=x; x=y; y=temp;} int r, c; double temp; for (r = 1; r < SIZE; r++) { // loop through rows for (c = 0; c < r; c++) { // loop columns below diagonal swapd(a[r][c], a[c][r]); // swap elements // swap(a[r][c], a[c][r]); // standard swap elements } } } void test () { alignas(64) // align by cache line size double matrix[SIZE][SIZE]; // define matrix transpose(matrix); // call transpose function } int main(){ clock_t start, stop; start = clock(); for(int i=0; i<liczba_powtorzen; i++){ test(); } stop = clock(); printf("\n time = %f ( %d cykli)", (stop - start)*1.0/CLOCKS_PER_SEC, (stop - start)); return 0; }
Strona 104.
Należy unikać zmiennych globalnych jeżeli to jest możliwe (lepsze cache'owanie).
Przykłady kiedy jest to wskazane:
- komunikacja pomiędzy wątkami,
- lookup-tables w funkcjach
Bez static stałe zmiennoprzecinkowe i tak będą umieszczone w globalnych stałych i za każdym razem kopiowane.
float SomeFunction (int x) { static float list[] = {1.1, 0.3, -2.0, 4.4}; return list[x]; }
Należy też unikać dynamicznego przydziału pamięci:
- fragmentacja pamięci
- wycieki pamięci
- garbage collection zajmuje dużo czasu
Jeżeli zbiór możliwych wartości jest skończony można zastąpić obliczenia lookup table
int factorial (int n) { // n! int i, f = 1; for (i = 2; i <= n; i++) f *= i; return f; }
int factorial (int n) { // n! // Table of factorials: static const int FactorialTable[13] = { 1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800, 39916800, 479001600}; if ((unsigned int)n < 13) return FactorialTable[n]; // Table lookup else return 0; // return 0 if out of range }
float a; bool b; a = b ? 1.0f : 2.5f;
float a; int b; static const float lookup[2] = {1.0f, 2.5f}; a = lookup[b];
int n; switch (n) { case 0: printf("Alpha"); break; case 1: printf("Beta"); break; case 2: printf("Gamma"); break; case 3: printf("Delta"); break; }
int n; static char const * const Greek[4] = { "Alpha", "Beta", "Gamma", "Delta" }; if ((unsigned int)n < 4) { printf(Greek[n]); }
const int size = 16; int i; float list[size]; ... if (i < 0 || i >= size) { cout << "Error: Index out of range"; } else { list[i] += 1.0f; }
if ((unsigned int)i < (unsigned int)size) { list[i] += 1.0f; } else { cout << "Error: Index out of range"; }
const int min = 100, max = 110; ... if (i >= min && i <= max) { ...
if ((unsigned int)(i - min) <= (unsigned int)(max - min)) { ...
enum Weekdays { Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday }; Weekdays Day; if (Day == Tuesday || Day == Wednesday || Day == Friday) { DoThisThreeTimesAWeek(); }
enum Weekdays { Sunday = 0x01, Monday = 0x02, Tuesday = 0x04, Wednesday = 0x08, Thursday = 0x10, Friday = 0x20, Saturday = 0x40 }; Weekdays Day; if (Day & (Tuesday | Wednesday | Friday)) { DoThisThreeTimesAWeek(); }
Jeżeli rozmiary wierszy macierzy są wielokrotnościami dwójki to obliczenia będą szybsze
const int rows = 10, columns = 8; float matrix[rows][columns]; int i, j; int order(int x); ... for (i = 0; i < rows; i++) { j = order(i); matrix[j][0] = i; }
Zapis
matrix[j][0]
// ogólny przypadek (int)&matrix[0][0] + j * (columns * sizeof(float)) // rozmiar wiersza jest wielokrotnością dwójki (int)&matrix[0][0] + j << 5
Czasami sztuczne powiększenie struktury aby jej rozmiar był potęgą dwójki może przyspieszyć działanie programu
struct S1 { int a; int b; int c; int UnusedFiller; // "Sztuczne" wypełnienie }; int order(int x); const int size = 100; S1 list[size]; int i, j; ... for (i = 0; i < size; i++) { j = order(i); // przeglądamy w zadanej kolejności list[j].a = list[j].b + list[j].c; }
strona 147.
strona 154.
program HelloWorld; #include( "stdlib.hhf" ) begin HelloWorld; stdout.put( "Hello, World of Assembly Language", nl ); end HelloWorld;
hla -v hw
static i8: int8; i16: int16; i32: int32 := -2130; u16: uns16 := 12455; isReal : boolean := true; c: char := 'c'; s: string := "Tekst"
procedure ProcName ; // lokalne deklaracje begin ProcName; // ciało funkcji end ProcName;
program zeroBytesDemo; #include( “stdlib.hhf” ); // Zeruje 256 elementów tablicy "intów" // której adres jest przekazywany EBX procedure zeroBytes; begin zeroBytes; mov( 0, eax ); mov( 256, ecx ); repeat mov( eax, [ebx] ); add( 4, ebx ); dec( ecx ); until( ecx = 0 ); // Repeat for 256 dwords. end zeroBytes; static dwArray: dword[256]; begin zeroBytesDemo; lea( ebx, dwArray ); call zeroBytes; // zeroBytes(); end zeroBytesDemo;
program PassByValueDemo; #include( "stdlib.hhf" ); var i: int32; j: int32; procedure pbv( a:int32; b:int32 ); var suma : int32; begin pbv; push( eax ); // a = -1; mov( -1, a ); // Store -1 into the “a” parameter. // b = -2; mov( -2, b ); // Store -2 into the “b” parameter. // Print the sum of a+b. mov( b, eax ); add( a, eax ); mov( eax, suma); stdout.put( "a+b=", suma, nl ); end pbv; begin PassByValueDemo; mov( 50, i ); mov( 25, j ); // Call pbv passing i and j by value pbv( i, j ); stdout.put ( "i= ", i, nl, "j= ", j, nl ); end PassByValueDemo;
program PassByRefDemo; #include( “stdlib.hhf” ); var i: int32; j: int32; procedure pbr( var a:int32; var b:int32 ); const aa: text := “(type int32 [ebx])”; bb: text := “(type int32 [ebx])”; begin pbr; push( eax ); push( ebx ); // Need to use EBX to dereference a and b. // a = -1; mov( a, ebx ); // Get ptr to the “a” variable. mov( -1, aa ); // Store -1 into the “a” parameter. // b = -2; mov( b, ebx ); // Get ptr to the “b” variable. mov( -2, bb ); // Store -2 into the “b” parameter. // Print the sum of a+b. // Note that ebx currently contains a pointer to “b”. mov( bb, eax ); mov( a, ebx ); // Get ptr to “a” variable. add( aa, eax ); stdout.put( “a+b=”, (type int32 eax), nl ); end pbr; begin PassByRefDemo; // Give i and j some initial values so // we can see that pass by reference will // overwrite these values. mov( 50, i ); mov( 25, j ); // Call pbr passing i and j by reference pbr( i, j ); // Display the results returned by pbr. stdout.put ( “i= “, i, nl, “j= “, j, nl ); end PassByRefDemo;
- BIST (Built-In Self Test) - sprzętowy test wewnętrznych struktur CPU
- ustalenie taktowania magistrali/CPU
- inicjalizacja urządzeń wbudowanych
- POST (Power On Self Test) - testy zapisane w BIOSie.
- "Bootowanie" - według ustalonej w BIOSie kolejności przeglądane są kolejne nośniki w poszukiwaniu tzw. bootsector-a.
- jeden procesor i jeden rdzeń,
- wszystkie rejestry są 16 bitowe, (32 bitowe po dodaniu przedrostka)
- adres wirtualny = adres fizyczny
- adres kodowany przez segment:offset
adres = segment * 16 + offset
W sumie 20 bitów (max 1MB pamięci) - brak ochrony pamięci i stronicowania
- zaawansowane funkcje (obsługa ekranu, klawiatury, dysków itd) dostępne przez przerwania BIOSu
- BIOS przegląda kolejne urządzenia zewnętrzne (dyskietki, dyski twarde, sieć) w poszukiwaniu nośnika startowego zawierającego tzw. bootsector.
- Bootsector (przeważnie 512 bajtów) jest to pierwszy sektor danego nośnika,
w którym na jego końcu umieszczono znacznik 0xAA55
(bajt 511 = 0xAA, bajt 512 = 0x55) - Bootsector jest ładowany do pamięci pod adres 0000:7c00 a następnie sterowanie jest przekazywane do pierwszej komórki tego obszaru
; Adres startowy 0000:7c00 [ORG 0x07c00] [BITS 16] mov ax, 0xb800 ; ustawiamy segment es na początek mov es,ax ; pamięci karty video mov byte [es:0],0x41 ; wpisujemy znak A w górny lewy róg mov byte [es:1],0x1f ; ustawiamy atrybuty (kolor i tło) loop1: jmp loop1 ; zapętlamy times 510 - ($-$$) db 0 ; uzupełniamy zerami do pozycji 510 dw 0x0aa55 ; wartość aa55 oznacza, ;że jest to sektor bootowalny
Kompilujemy poleceniem
nasm boot1.asm -fbin -o boot1.bin
Tak przygotowany bootsector możemy przekopiować do pierwszego sektora dysku, pendrive czy innego nośnika np. poleceniem
dd if=./boot1.bin of=/dev/sdb1 bs=512 count=1
Można też tak przygotowany plik uruchomić bezpośrednio w emulatorze np.
qemu -hda ./boot1.bin
BIOS (Basic Input/Output System) to zapisany w pamięci stałej
zestaw podstawowych procedur zapewniających podstawową komunikację z
urządzeniami zewnętrznymi tj. ekran, klawiatura, dyski.
Komunikacja z BIOS-em odbywa się przez przerwania.
Lista przerwań BIOS-a.
Lista dostępnych przerwań zależy od płyty głównej oraz od
wersji BIOS-u wgranej do pamięci EPROM.
Przerwanie 0x10 w głównej mierze jest odpowiedzialne za wyjście na ekran i obsługę klawiatury. Numer wybranej funkcji umieszczamy w rejestrze AH
[ORG 0x07c00] [BITS 16] mov ax, 0 mov es, ax ; ustawienie segmentu ES na zero mov ah, 0x03 ; pobranie aktualnej pozycji kursora mov bh, 0 ; strona 0 int 0x10 ; wynik będzie w dh (wiersz) dl (kolumna) mov ah, 0x13 ; wypisanie tekstu mov al, 0x01 ; tryb pisania : bit 0 - przesunąc kursor po zapisie ; bit 1 - tekst zawiera na przemian litery i atrybuty znaków mov cx, msglen ; długość tekstu mov bh, 0x00 ; strona ekranu mov bl, 0x07 ; atrybuty znaków (biały na czarnym tle) mov bp, msg ; wskaźnik na tekst ES:BP ; mov dx, 0x0000 ; gdzie wypisać (górny lewy róg) int 0x10 loop1: hlt ; zatrzymujemy procesor jmp loop1 ; zapętlamy msg: db "Pozdrowienia z bootloadera! ", 13, 10, 0 msglen equ ($-msg-1) times 510 - ($-$$) db 0 ; uzupełniamy zerami do pozycji 510 dw 0x0aa55 ; wartość aa55 oznacza, ;że jest to sektor bootowalny
Przerwanie 0x13 zapewnia dostęp do dysku.
Możemy wczytywać dany sektor dysku podająć kolejno numer cylindra, głowicy i sektoru. Ten tryb adresowania oznacza się przez CHS (Cylinder-Head-Sector). Jednakże wygodniej jest stosować tryb LBA (Logical block addressing) który każdemu sektorowi nadaje logiczny adres, który potem jest przeliczany na adres CHS wedlug wzoru
LBA = ( numer_cylindra * liczba_glowic_na_cylinder + numer_glowicy ) * liczba_sektorow_na_sciezke + numer_sektora -1
mov ax, 0 mov ds, ax ; ustawienie segmentu DS na zero mov ah, 0x42 ; odczyt LBA mov dl, 0x80 ; numer dysku (dysk nr 0) mov si, read_pocket ; DS:SI adres struktury definiujacej ile przeczytać i gdzie umieścić int 0x13 ;... read_pocket: db 0x10 ; rozmiar rekordu (pocket) db 0 ; zarezerwowane = 0 dw 1 ; ile sektorów odczytać dd 0x00007E00 ; gdzie umieścić wynik dd 1 ; który sektor odczytać dd 0 ; starsze bajty nr. sektora
Przykład: Bootloader wczytuje drugi sektor dysku i wykorzystuje zawarte w nim informacje.
Biblioteka jest ładowana do raz pamięci i może być współdzielona pomiędzy różne procesy. Segment danych globalnych jest powielany dla każdego procesu.
Jest mapowana w pamięci pod różnymi adresami dla różnych procesów.
Potrzebny jest kod który będzie działał niezależnie gdzie się znajduje.
mov eax,[zmienna] ; BŁĄD!!!
Zmienne nie są pod stałymi adresami, są w pamięci zwanej Global Offset table (GOT), która jest usytuowana w stałej odległości od kodu biblioteki współdzielonej.
Aby uzyskać adres absolutny GOT wykonujemy
extern _GLOBAL_OFFSET_TABLE_ func: push ebp mov ebp,esp push ebx call .get_GOT .get_GOT: pop ebx add ebx,_GLOBAL_OFFSET_TABLE_+$$-.get_GOT wrt ..gotpc ; the function body comes here mov ebx,[ebp-4] mov esp,ebp pop ebp ret
lea eax,[ebx+myvar wrt ..gotoff]
myvar wrt ..gotoff oblicza offset zmiennej lokalnej myvar od początku GOT
lea eax,[ebx+extvar wrt ..got]
myvar wrt ..gotoff oblicza offset zmiennejzewnętrznej extvar od początku GOT
W trybie 64 bitowym jeżeli zmienna znajduje się w nie dalej niż +/- 2GB można użyć adresowania relatywnego do RIP
lea rax,[rel myvar] mov [rel myvar], rbx
Odwołania do funkcji zewnętrznych odbywa się przy pomocy procedure linkage table (PLT)
CALL printf WRT ..plt
- Początkowy stan rejestrów
- Dostępne adresy (48 bit)
- Organizacja pamięci wirtualnej
objdump -x hello64
Nagłówki w pliku wykonywalnym
hello64: file format elf64-x86-64
hello64
architecture: i386:x86-64, flags 0x00000112:
EXEC_P, HAS_SYMS, D_PAGED
start address 0x00000000004000b0
Program Header:
LOAD off 0x0000000000000000 vaddr 0x0000000000400000 paddr 0x0000000000400000 align 2**21
filesz 0x00000000000000d2 memsz 0x00000000000000d2 flags r-x
LOAD off 0x00000000000000d4 vaddr 0x00000000006000d4 paddr 0x00000000006000d4 align 2**21
filesz 0x0000000000000006 memsz 0x0000000000000006 flags rw-
Sections:
Idx Name Size VMA LMA File off Algn
0 .text 00000022 00000000004000b0 00000000004000b0 000000b0 2**4
CONTENTS, ALLOC, LOAD, READONLY, CODE
1 .data 00000006 00000000006000d4 00000000006000d4 000000d4 2**2
CONTENTS, ALLOC, LOAD, DATA
SYMBOL TABLE:
00000000004000b0 l d .text 0000000000000000 .text
00000000006000d4 l d .data 0000000000000000 .data
0000000000000000 l df *ABS* 0000000000000000 hello64.asm
00000000006000d4 l .data 0000000000000000 tekst
0000000000000006 l *ABS* 0000000000000000 dlugosc
0000000000000000 l df *ABS* 0000000000000000
00000000006000d8 l O .data 0000000000000000 _GLOBAL_OFFSET_TABLE_
00000000004000b0 g .text 0000000000000000 _start
00000000006000da g .data 0000000000000000 __bss_start
00000000006000da g .data 0000000000000000 _edata
00000000006000e0 g .data 0000000000000000 _end
Odwołania do funkcji zewnętrznych odbywa się przy pomocy procedure linkage table (PLT)
CALL printf WRT ..plt
Tomasz Kapela, Kraków 2011-2020
 .
.